Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.4 - Ex. 5
Use os gráficos de e e suas retas em para encontrar
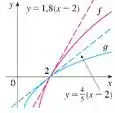
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar o limite do quociente das funções e , quando tende a , usando os gráficos dessas funções.
Repare que ele nos deu também as retas tangentes à curva:
E
Dessa forma, a gente consegue inferir que dá pra calcular esse limite usando a regra de L’Hospital. Assim, a gente deriva numerador e denominador separadamente e compara com o valor obtido pela expressão da reta tangente no ponto .
Vamos lá!
Passo 2
Usando a regra de L’Hospital, vamos ter:
E como o limite do quociente é o quociente dos limites, temos:
Agora, como o coeficiente angular da reta tangente no ponto é equivalente ao valor da derivada nesse ponto, vamos ter:
E
Então, substituindo no limite, ficamos com:
Fazendo essa divisão, temos:
Valeu, galera! Até a próxima! 😉