Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.2 - Ex. 7
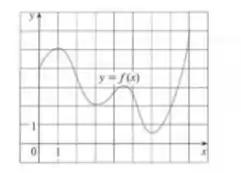
Use o gráfico de para estimar os valores de que satisfaçam a conclusão do Teorema do Valor Médio para o intervalo [0,8].
Passo 1
Opa! Bora pra mais uma?
O problema nos da um gráfico e pede pra a gente estimar os valores de que satisfaçam a conclusão do Teorema do Valor Médio para o intervalo [0,8]:
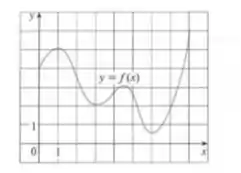
Antes de tudo vamos ver se as condições para o Teorema do Valor Médio (TVM) são satisfeitas.
Temos que é contínua em [0,8], pois, perceba que não temos nenhuma descontinuidade. Como assim?! Segue a curvinha do gráfico, não temos nenhum buraquinho nele, ele ta ligadinho certinho até o final do intervalo.
Temos também que é derivável no intervalo dado, não temos nenhum “bico”, nenhuma quebra repentina onde a reta tangente a curva seria vertical.
Como é derivável e contínua, teremos que:
Passo 2
Beleza, vamos então encontrar esse ?!
A malha do gráfico é de 1x1 (cada linha que a gente subir, vai ter uma unidade, e cada coluna que deslocarmos, também terá uma unidade), então vamos lá, teremos que:
Passo 3
Ok, agora, para quais valores de teremos esse valor do TVM. Esse valor do TVM nada mais é que a inclinação das retas traçadas tangencialmente nos pontos de inversão do gráfico, ou seja, nos picos e vales do gráfico.
Assim, teremos um que satisfaça para, aproximadamente,
Resposta
Temos, .