Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 8
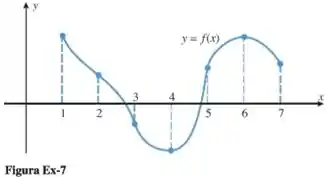
Use o gráfico do Exercício 7 para fazer uma tabela que mostre os sinais de e nos intervalos e .
Passo 1
Precisamos avaliar os sinais das derivadas primeira e segunda de em cada intervalo.
Pra isso, precisamos saber que:
- A derivada primeira tem sinal positivo nos intervalos em que a função é crescente (“sobe” da esquerda pra direita), e sinal negativo quando decrescente (“desce” da esquerda pra direita).
- A derivada segunda é positiva nos intervalos em que a função tem concavidade voltada pra cima; sinal negativo nos intervalos com concavidade pra baixo.
Com essas informações já podemos construir a tabela facilmente. Vamos ter:
Resposta
Exercícios de Livros Relacionados
Use a definição 4.1.1 para provar que f x = x 2 é crescente em 0 ,+ ∞ .
57. a) Prove que o polinômio cúbico geral: f x = a x 3 + b x 2 + c x + da ≠ 0 Tem exatamente um ponto de inflexão.b) Prove que, se o polinômio cúbico tiver três cortes com o eixo x , o ponto de inflex
47-48. Use um recurso computacional para gerar os gráficos de f ' e f ' ' no intervalo indicado; use os gráficos para estimar as coordenadas x dos pontos de inflexão de f , os intervalos nos quais f é
(a) Explique por que a regra de L’Hôpital não se aplica ao problema lim x → 0 x 2 sin 1 x sin x (b) Encontre o limite
O modelo de crescimento logístico dado na Fórmula (1) é equivalente a: y e k t + A y = L e k t Em que y é a população no instante t t ≥ 0 e A , k e L são constantes positivas. Use a derivação implícit