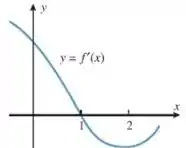
Use o gráfico de na figura seguir para substituir a interrogação por , ou , conforme apropriado. Explique seu raciocínio.
(a) (b) (c) (d)
(e) (f)
Passo 1
(a)Aqui, temos que avaliar se o valor da função em 0 é maior, igual ou menor que o valor da função em 1.
Pelo gráfico fica fácil de ver que a função em tem valor maior que quando . Logo,
Passo 2
(b)Pelo gráfico é perceptível que é maior que , que equivale a um valor negativo. Então:
Passo 3
(c)Observando o ponto em que o gráfico corta o eixo das ordenadas, que é o valor de , vemos que o gráfico decresce. Logo, a derivada é negativa.
Sendo esse ponto do gráfico não um ponto de mínimo e nem de máximo, é diferente de zero. Temos que:
Passo 4
(d)O mesmo de (c) vale aqui: o gráfico em decresce, logo a derivada é negativa. E não estando em ponto de máximo ou de mínimo, não pode equivaler a zero. Assim:
Passo 5
(e)Aqui avaliamos a derivada segunda no ponto . O sinal da derivada segunda indica a concavidade do gráfico: sendo positiva, concavidade voltada pra cima; sendo negativa, voltada pra baixo.
Nesse ponto, a concavidade está voltada pra cima, logo tem sinal positivo. Portanto, maior que zero.
Pra valer zero, uma derivada segunda de um ponto deve ocorrer no ponto de inflexão da função, que é o ponto de inversão da concavidade!
Passo 6
(f)Da mesma forma que no item anterior, estamos em um ponto, , em que a concavidade do gráfico é voltada pra cima. Logo, não é um ponto de inflexão, e, assim, a derivada segunda é positiva.
Resposta
(a)
(b)
(c)
(d)
(e)
(f)