Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 14
Use o gráfico da função para dizer o valor de cada limite, se exisitir. Se não existir, explique por quê .
a)
b)
c)
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a função
E nosso objetivo é encontrar os valores de , e a partir do gráfico de .
Tem ideia de como fazemos isso?
O limite de uma função é nada mais do que o valor que a função tende a assumir quando se aproxima de um certo valor.
Então vamos esboçar o gráfico da função e analisar os valores que a função tende a assuir em , e .
Veja só!
Passo 2
Vamos começar esboçando a função
Quando , . Perceba que para , a função é sempre negativa já que .
A partir de a função é positiva pois tanto o numerador quanto o denominador são positivos.
Simplificando a função, temos
Portanto a função terá essa cara, mas por conta da simplificação, consideramos que , então na verdade o lado negativo de será invertido para o ...
Montando as peças desse quebra-cabeça, nossa função terá a mesma cara de porem deslocado uma unidade para a esquerda já que temos no lugar de .
Além disso, vamos pegar a parte negativa de e inverter para a parte negativa de .
Dessa forma, nossa função será dada por
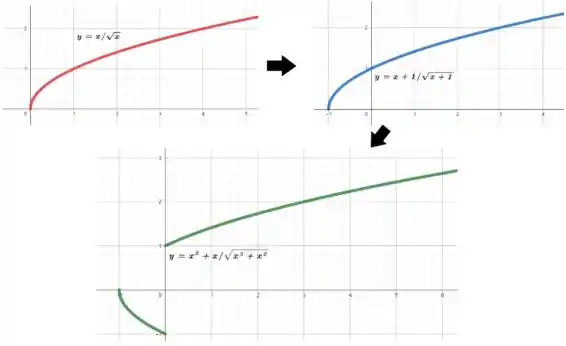
Tranquilo até aqui?
Passo 3
Agora vamos observar nossa função e determinar os valores dos limites que foram pedidos...
No item a) queremos
Ou seja, o valor que assume quando tende a pela esquerda...
Perceba que em a função tende a , portanto
Show?
Passo 4
No item b), queremos obter , ou seja, o valor que tende a assumir quando tende a pela direita...
Pelo gráfico, percebemos que como agora é positivo, tende a , logo
Bacana, não é?
Passo 5
Por fim, no item c) queremos obter o valor de .
Aqui vamos aplicar uma propriedade importante... percebeu que os limites laterais de em não são os mesmos?
Quando isso acontece, podemos afirmar que o limite naquele ponto não existe pois ele diverge.
Logo, como
É isso! Entendeu tudo? Responde Aí
Resposta
a)
b)
c)