Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.8 - Ex. 1
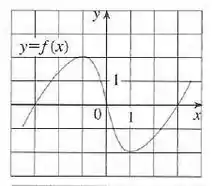
Use ao gráficos dados para estimar o valor de cada dereivada. Esboce então o gráfico de .
Passo 1
Fala aí, galerinha!
Nesse problema foi dado um gráfico de uma função e nosso objetivo é determinar o valor da derivada dessa função em alguns pontos.
Parece complicado?
Para resolver esse problema temos que lembrar que a derivada de uma função em um ponto pode ser interpretada como a inclinação da reta tangente à função naquele ponto.
Lembra disso?
Então para obter os resultados, vamos traçar as retas tangentes à e determinar suas inclinações.
Para determinar a inclinação de uma reta precisamos de dois pontos distintos pertencentes a essa reta. Com isso podemos determinar sua inclinação (coeficiente angular) como
Antes de começar, podemos perceber que é uma função ímpar pois possui simetria com a origem do sistema.
Dessa forma podemos simplificar nossos cálculos pois para qualquer . Como o problema pede para pontos positivos e negativos, podemos calcular apenas um deles e cortar um tempo da nossa solução!
Sabou? Bora começar!
Passo 2
Vamos começar por e
Traçando a reta tangente a em , temos
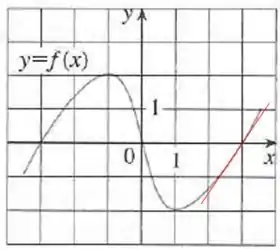
Quando , o próximo ponto vai ter que ser aproximado...
Podemos dizer que quando , aproximadamente.
Dessa forma temos que a derivada
Tranquilo até aqui?
Passo 3
Para e fica um pouquinho mais difícil:
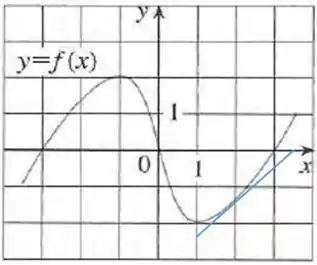
Determinando os pontos que pertencem à reta, vamos aproximar os pontos e
Show?
Passo 4
Vamos analisar agora os pontos e
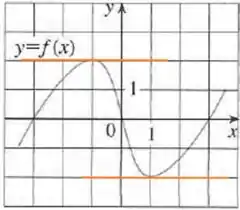
Olhando o gráfico podemos perceber que quando e temos um ponto de máximo e mínimo respectivamente.
Isso significa que suas retas tangentes são horizontais e portanto, suas inclinações são nulas.
Estamos quase lá!
Passo 5
No ponto temos:
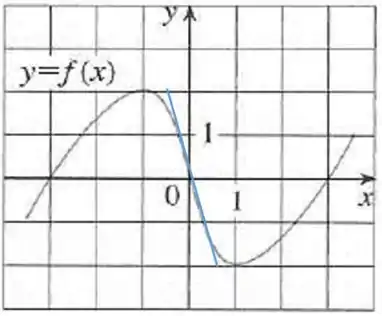
Temos o ponto e podemos aproximar
Legal, né?
Passo 6
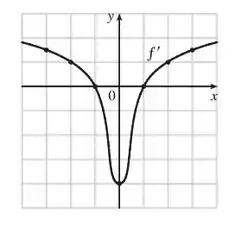
Por fim, temos que fazer o esboço de .
Como é uma função impar, consequentemente será uma função par, ou seja, será simétrico em relação ao eixo .
Vimos que em , , e .
Esboçando esses pontos e traçando uma curva que ligue eles de forma harmônica, podemos encontrar algo parecido com
E aí! entendeu tudo? Responde Aí!