Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 6
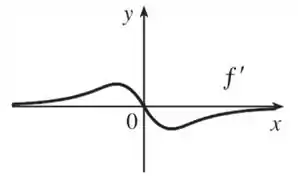
Trace ou copie o gráfico da função dada. (Suponha eixos com a mesma escala.) Use então o método do Exemplo para esboçar o gráfico de .
Passo 1
Fala galerinha! Vamos treinar as nossas habilidades envolvendo gráficos de funções e suas derivadas!
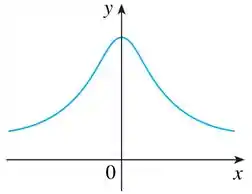
Para esboçar o gráfico da derivada, temos que prestar atenção em alguns pontos do gráfico original que é esse aqui:
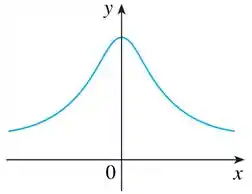
Nos intervalos onde a função decresce, a derivada será negativa. Nos casos em que cresce, será positiva, não se esqueçam!
Bora ver isso com calma. Vem que te ajudo.
Passo 2
Vale ressaltar que, quanto mais rápido a função estiver aumentando ou diminuindo, mais longe o eixo estarão os pontos correspondentes no gráfico da derivada, isso porque ela é a inclinação da reta tangente.
Fechou?
Além disso, temos que procurar os pontos onde temos uma tangente na horizontal – como a derivada é a inclinação da reta tangente, nesses pontos, a será zero.
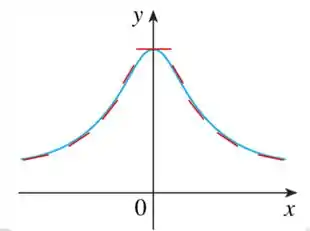
Vamos procurar essas características no gráfico. No desenho abaixo, as setas em vermelho indicam se o trecho está crescendo ou decrescendo, enquanto as retas tangentes estão representadas em preto. Dá uma olhadinha em como ficou nosso diagrama:
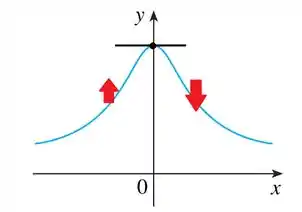
E algumas retas tangentes podem ser:
Passo 3
Agora sim! Podemos desenhar o gráfico de com o que a gente já descobriu do gráfico de ! Só precisamos seguir as regras ditas no início do passo . Dá uma olhada em como vai ficar a comparação entre o gráfico original e o da sua derivada:
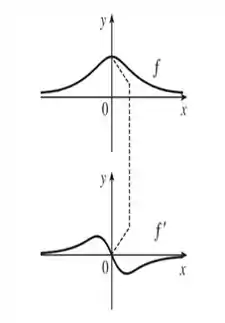
Pronto! Esse vai ser o nosso esboço de , beleza? ;)
Resposta
O esboço de será o seguinte:
