Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 26
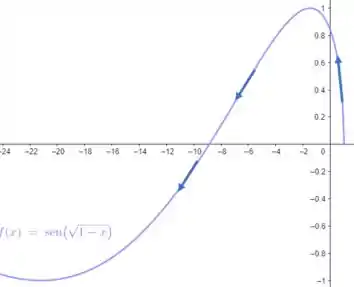
Use os gráficos de e para esboçar a curva parametrizada e . Indique com setas a direção na qual a curva é traçada quanto aumenta.
Passo 1
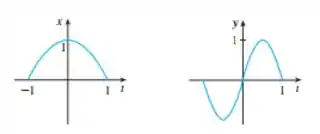
Faaalaeee, beleza??? Bom... o enunciado nos deu os seguintes gráficos:
Perceba que temos e , ou seja, temos uma função parametrizada por aí, né?
E queremos esboçar essa curva!!!
Para isso, primeiro temos que descobrir que funções são essas que são mostradas nos gráficos para depois igualarmos para que temos uma função no formato ou .
Por fim, vamos imaginar alguns valores (em ordem crescente) de e ver quando a função vai crescer.
Agora bora lá!! 😉
Passo 2
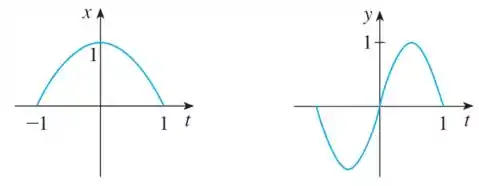
Vamos analisar essa primeira curva:
Temos que observar que é uma parábola com a concavidade para baixo e descolado para cima em unidade, então podemos dizer que ela se comporta assim:
Passo 3
Agora vamos para a segunda curva:
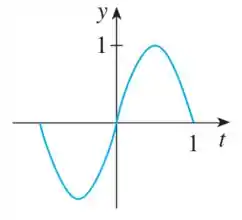
Vemos que é uma função senoidal.
Podemos escrever como seno ou cosseno, só tomando cuidado com a fase que adicionamos essas funções, afinal:
Vamos escrever nossa função do jeito mais fácil então
Passo 4
Isolando na equação do passo 2, temos:
Se substituirmos na equação do passo 3, obtemos:
Passo 5
Plotando a nossa curva, obtemos:
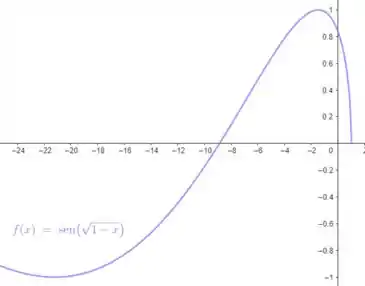
Agora vamos analisar o que acontece quando aumenta:
Se pegarmos um intervalo de nossa função fica
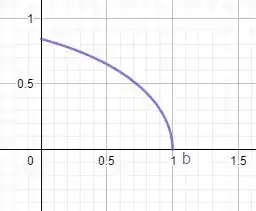
Se formos aumentando esse intervalo de , por exemplo de , vamos ver isso:
Então por isso podemos falar que a orientação dessa parábola é no sentido anti-horário
Esse exercício requer apenas que testemos nossos conhecimentos de gráficos, conforme você for testando com mais funções, mais vai pegando o jeito. Terminamos por aqui, te vejo na próxima resolução 😉
Resposta
