Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 5.3 - Ex. 12
(a) Se e , use a informação do exemplo 4 para mostrar que o sistema é subamortecido quando o coeficiente de amortecimento satisfaz , mas a ressonância pode ocorrer somente se .
(b) Construa a curva de ressonância do sistema quando
Passo 1
(a) E aíí meu jovem, vamos lá
O modelo de uma equação diferencial para esses casos é:
No caso temos e :
Que tem como equação auxiliar:
As raízes dessa equação auxiliar são
Se , temos
E dessa forma, o sistema é subamortecido
Passo 2
(b) Temos
Se , temos:
Que tem a curva dada da seguinte forma, para diferentes valores de :
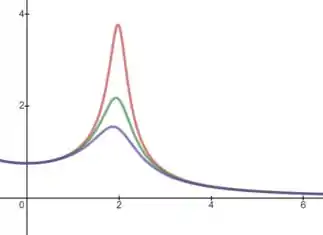
Resposta
b) 
Exercícios de Livros Relacionados
Uma massa de 100 g é atada a uma mola de constante elástica 0,016 N/cm. Após a massa atingir o equilíbrio, seu suporte oscila de acordo com a fórmula h t = s e n ( 8 t ) , em que h representa o desloc
No problema 3, determine a equação do movimento se a força externa for f t = e - t . s e n ( 4 t ) . Analise o deslocamento quando t → ∞ .
Uma massa de 0,5 kg é atada a uma mola que tem constante de elasticidade igual a 6 N/m. A massa parte do repouso 2 m abaixo da posição de equilíbrio e o movimento subsequente está sujeito a uma força
Resolva a equação diferencial do problema precedente se a mola distende-se 4 cm com um peso de 0,5 kg, e β = 2 , h t = 5 . c o s ( t ) , x 0 = x ' 0 = 0
Uma massa de 1 kg é atada a uma mola cuja constante vale 5 N/m. A massa é solta 1 cm abaixo da posição de equilíbrio com uma velocidade de 5 cm/s para baixo. O movimento subsequente tem lugar em um me