Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.2 - Ex. 19
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir:
Passo 1
Temos a seguinte imagem gráfica:
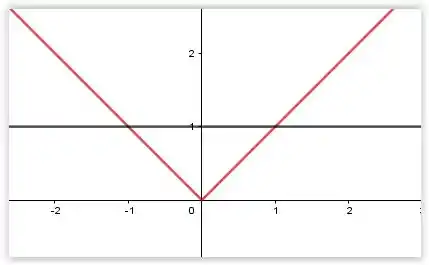
Temos que logo e . Então podemos concluir que nossa .
Podemos perceber no gráfico que a variação no eixo y é
Queremos usar o método da casca, porém a rotação agora é em torno do eixo x, logo, devemos usar a seguinte fórmula:
Em que .
Substituindo da fórmula acima, temos:
Resposta
Exercícios de Livros Relacionados
Na Figura abaixo, a região limitada pelo eixo x, pela reta x = 1 e pela curva y = x 2 é denotada por R1; a região limitada pelas curvas y = x 2 e y 2 = x é denotada por R2; a região limitada pelo eixo
Nos Exercícios de 21 a 24, a região é limitada pelas curvas x = y 2 - 2 e x = 6 - y 2 gira em torno do eixo indicado. Ache o volume do sólido gerado.22. o eixo y
Na Figura abaixo, a região limitada pelo eixo x, pela reta x = 1 e pela curva y = x 2 é denotada por R1; a região limitada pelas curvas y = x 2 e y 2 = x é denotada por R2; a região limitada pelo eixo
Na Figura abaixo, a região limitada pelo eixo x, pela reta x = 1 e pela curva y = x 2 é denotada por R1; a região limitada pelas curvas y = x 2 e y 2 = x é denotada por R2; a região limitada pelo eixo
Na Figura abaixo, a região limitada pelo eixo x, pela reta x = 1 e pela curva y = x 2 é denotada por R1; a região limitada pelas curvas y = x 2 e y 2 = x é denotada por R2; a região limitada pelo eixo