Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 22

Nos Exercícios de 21 a 24, a região é limitada pelas curvas x = y 2 - 2 e x = 6 - y 2 gira em torno do eixo indicado. Ache o volume do sólido gerado.

22. o eixo y

Passo 1

Primeiro vamos ver como fica a região.

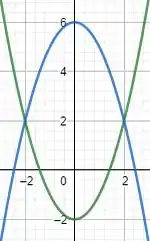
Como essa figura está girando em torno do eixo y e ela é simétrica em relação ao eixo x, podemos calcular o volume da parte acima do eixo x e multiplicar por 2, obtendo o volume total.

Para essa situação vamos usar o método dos anéis circulares, onde nosso anel imaginário estaria na horizontal e a espessura do anel é dy, então temos eu:

d V = π ( R 2 - r 2 ) ⋅ d y

Onde R é o raio maior do anel e r é o raio menor.

Então como o d V depende de d y precisamos achar R e r como funções da forma f ( y ) .

Assim:

r = y 2 - 2           R = 6 - y 2

Logo:

V = 2 π ∫ 0 2 6 - y 2 2 - y 2 - 2 2   d y

Os limites de integração são esses já que y varia de 0 a 2 na região limitada

Passo 2

Agora resolvendo a integral.

V = 2 π ∫ 0 2 6 - y 2 2 - y 2 - 2 2 d y

= 2 π ∫ 0 2 36 - 12 y 2 + y 4 - y 4 + 4 y 2 - 4 d y

= 2 π ∫ 0 2 32 - 8 y 2   d y

= 2 π 32 ∫ 0 2   d y - 8 ∫ 0 2 y 2   d y

= 2 π 32 y 0 2 - 8 y 3 3 0 2

= 2 π 32 2 - 0 - 8 1 3 2 3 - 0

= 2 π 64 - 64 3

= 2 π 128 3 = 256 3 π

Resposta

V = 256 3 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o volume do solido gerado por rotação, em torno do eixo y da região limitada pela curva y = x 4 , a reta x= 1 e eixo x
Ache o volume do sólido gerado se a região do Exercício 25 for rotacionada em torno do eixo y.
Ache o volume do sólido gerado pela rotação da região do Exercício 32 em torno do eixo y.
Ache o volume do sólido gerado pela rotação da região do Exercício 30 em torno da reta x = 2 .
Ache o volume do sólido gerado pela rotação da região limitada pelo gráfico de y = 4 x - 1 8 x 4 , pelo eixo y e pela reta y = 6 em torno da reta x = 2 .