Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.2 - Ex. 19

  1. Use o método de Euler com cada um dos passos dados para estimar o valor de y 0,4 onde y é a solução do problema de valor inicial y ' = y ,   y 0 = 1 .
    1. h=0,4
    2. h=0,2
    3. h=0,1

  2. Sabemos que a solução exata do problema de valor inicial na parte (a) é y = e x , 0 ≤ x ≤ 0,4 , junto com as aproximações de Euler, usando os passos da parte (a). Use seus esboços para decidir se suas estimativas na parte (a) estão subestimadas ou superestimadas.
  3. O erro no método de Euler é a diferença entre o valor exato e o valor aproximado. Calcule os erros feitos na parte (a) ao usar o método de Euler para estimar o verdadeiro valor de y ( 0,4 ) ; a saber, e 0,4 .   O que acontece com o erro cada vez que o passo cai pela metade?

Passo 1

  1. De acordo com o método de Euler:       y x + h ≈ y x + h d y d x

    2. Nós sabemos que y 0 = 1 , precisamos encontrar y ( 0,4 )

    1. Para encontrar y ( 0,4 ) com h = 0,4 , nós precisamo usar a fórmula:

      2. y x + h ≈ y x + h d y d x

      Substituindo x = 0 , d y d x = y ' 0 = y 0 = 1

      Teremos que y 0 + 0,4 ≈ y 0 + 0,4   1 ≈ 1 + 0,4 = 1,4

      Então, y 0,4 = 1,4

      Passo 2

    2. Para encontrar encontrar y ( 0,4 ) com h = 0,2 , nós precisamo usar a fórmula do método de Euler duas vezes: primeiro nós vamos encontrar y 0 + 0,2 = y ( 0,2 ) usando y 0   e h = 0,2 . Depois iremos usar y ( 0,2 ) e h = 0,2 para encontrar y 0,2 + 0,2 = y ( 0,4 )

      3. y x + h ≈ y x + h d y d x

      Aqui, temos que x = 0 , d y d x = y ' 0 = y 0 = 1

      Então: y 0 + 0,2 ≈ y 0 + 0,2 y 0 ≈ 1 + 0,2 = 1,2

      y 0,2 = 1,2

      Passo 3

      Agora vamos aplicar a fórmula pela segunda vez:

      y x + h ≈ y x + h d y d x

      Fazendo x = 0,2 ,     d y d x = y ' 0,2 = y 0,2 = 1,2 ficamos com:

      y 0,2 + 0,2 ≈ y 0,2 + 0,2 y 0,2 ≈ 1,2 2 = 1,44

      Então concluímos que y 0,4 = 1,44

      Passo 4

    3. Para encontrar     y ( 0,4 ) com   h = 0,1 nós precisaremos usar a fórmula do método de Euler quatro vezes:

    Primeiro encontraremos y 0 + 0,1 = y ( 0,1 ) usando   y ( 0 ) e h = 0,1

    Depois iremos usar y ( 0,1 ) e h = 0,1 para encontrar y 0,1 + 0,1 = y ( 0,2 )

    Então iremos encontrar y 0,2 + 0,1 = y ( 0,3 ) usando y 0,2 e h = 0,1

    Por último, vamos usar y 0,3 e h = 0,1 para achar y 0,3 + 0,1 = y ( 0,4 )

    y x + h ≈ y x + h d y d x

    Então vamos lá para a primeira substituição: x = 0 , d y d x = y ' 0 = y 0 = 1   e   h = 0,1

    y 0 + 0,1 ≈ y 0 + 0,1 y 0 ≈ 1 + 0,1 = 1,1

    y 0,1 = 1,1

    Passo 5

    Agora faremos x = 0,1 , d y d x = y ' 0,1 = y 0,1 = 1,1   e   h = 0,1

    y 0,1 + 0,1 ≈ y 0,1 + 0,1 y 0,1 ≈ 1,1 2 = 1,21

    y 0,2 = 1,21

    Passo 6

    Na nossa terceira substituição temos x = 0,2 , d y d x = y ' 0,2 = y 0,2 = 1,21   e   h = 0,1

    y 0,2 + 0,1 ≈ y 0,2 + 0,1 y 0,2 ≈ ( 1,21 ) ( 1,1 ) = 1,331

    y 0,3 = 1,331

    Passo 7

    Ufa! Só mais uma vez... agora x = 0,3 , d y d x = y ' 0,3 = y 0,3 = 1,331   e   h = 0,1

    y 0,3 + 0,1 ≈ y 0,3 + 0,1 y 0,3 ≈ ( 1,331 ) ( 1,1 ) = 1,4641

    y 0,4 = 1,4641

    Passo 8

  2. Fazendo o gráfico de y = e x e da parte (a) do exercício ( h = 0,1 ; h = 0,2 ; h = 0,4 ) ficamos com:

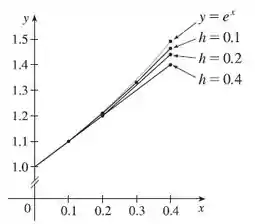
    3. Podemos ver que todas nossas estimativas estão subestimadas, pois estão abaixo do gráfico de y = e x .

    Passo 9

  3. Queremos calcular o erro feito na parte (a) do exercício para estimar qual seria o verdadeiro valor de y ( 0,4 ) . Para isso, precisamos fazer a difereça entre o valor exato e o valor aproximado:
  1. Para h = 0,4 : (valor exato) – (valor aproximado) = e 0,4 - 1,4 ≈ 0,0918
  2. Para h = 0,2 : (valor exato) – (valor aproximado) = e 0,4 - 1,4 4 ≈ 0,0 518
  3. Para h = 0 , 1 : (valor exato) – (valor aproximado) = e 0,4 - 1,4 641 ≈ 0,0 277

Note que cada vez que o passo ( h ) é reduzido pela metade, o erro também é reduzido pela metade.

Resposta

  1. (i) y 0,4 = 1,4

    2. (ii) y 0,4 = 1,44

    (iii) y 0,4 = 1,4641

  2. Subestimadas.
  3. O erro cai pela metade.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 26 a 33, desenhe um campo de direções para a equação diferencial dada. Baseado no campo de direções, determine o comportamento de y quando t → ∞ . Se esse comportamento dep
Em cada um dos problemas de 26 a 33, desenhe um campo de direções para a equação diferencial dada. Baseado no campo de direções, determine o comportamento de y quando t → ∞ . Se esse comportamento dep
Em cada um dos problemas de 26 a 33, desenhe um campo de direções para a equação diferencial dada. Baseado no campo de direções, determine o comportamento de y quando t → ∞ . Se esse comportamento dep
D 3 + D 2 + D - 1 às seguintes funções:
D 3 + D 2 + D - 1 às seguintes funções: