Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.4 - Ex. 6
Use o método do Exercício para encontrar um número tal que se .
Passo 1
Então galera, se esboçarmos o gráfico de teremos:
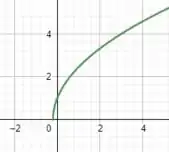
Agora para encontrarmos o temos que fazer:
Que é equivalente a:
Vale ressaltar que só tiramos o módulo aqui, ok? Bora continuar!
Passo 2
Para termos a igualdade , temos que tem que valer:
E para termos a igualdade , temos que tem que valer:
Sendo assim, o nosso delta mínimo será:
Resposta
Exercícios de Livros Relacionados
Nos Exercícios de 1 a 22, faça um esboço do gráfico e ache o limite indicado, se existir, se não existir, indique a razão disto. 5 )F x = { x ² ,s ex ≤ 2 8 - 2 x ,s e2x ² a ) lim x → 2 + F x ; b ) l
Nos Exercícios de 1 a 22, faça um esboço do gráfico e ache o limite indicado, se existir, se não existir, indique a razão disto. 2 )f x = { - 2 ,s ex0 2 ,s e0 ≤ x a ) lim x → 0 + f x ; b ) lim x → 0
Nos Exercícios de 1 a 22, faça um esboço do gráfico e ache o limite indicado, se existir, se não existir, indique a razão disto. 9 )f x = { x ² - 4 ,s ex2 4 ,s ex = 2 4 - x ² ,s e2x ² ² a ) lim x → 2
Nos Exercícios de 1 a 22, faça um esboço do gráfico e ache o limite indicado, se existir, se não existir, indique a razão disto. 1 0 )f x = { 2 x + 3 ,s ex1 4 ,s ex = 1 x ² + 2 ,s e1x ² a ) lim x → 1
Nos Exercícios de 1 a 22, faça um esboço do gráfico e ache o limite indicado, se existir, se não existir, indique a razão disto. 1 2 )f x = 3 + | 2 x - 4 | a ) lim x → 2 + f x ; b ) lim x → 2 - f