3. a) Encontre os valores de e na figura anexa.
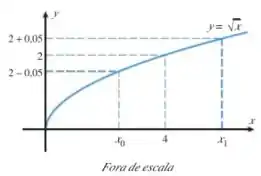
b) Encontre um número positivo , tal que se .
Passo 1
a) Então pessoal, se prestarmos atenção no gráfico notaremos que está associado ao seguinte valor de :
Mas a função é definida como:
Dessa forma, para temos que vale:
Passo 2
Da mesma forma que fizemos com , temos que está associado ao seguinte valor de :
Mas a função é definida como:
Dessa forma, para temos que vale:
Passo 3
b) Então galera, o que temos que encontrar é um valor de delta mínimo que satisfaça as condições dadas, beleza? De acordo com os valores que encontramos na letra a), temos:
E está aí! 😉
Resposta
a)
b)