Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.3 - Ex. 6
Nos Exercícios de 1 a 22, faça um esboço do gráfico e ache o limite indicado, se existir, se não existir, indique a razão disto.
Passo 1
Para começar precisamos desenhar o gráfico para a nossa função . Feito isso, vamos avaliar os limites laterais e, se existir, o limite bilateral.
Desenhando o gráfico:
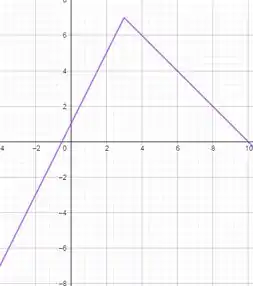
O próximo passo é descobrir os limites.
Passo 2
Podemos olhar no gráfico para achar o limite direito, ou seja, o limite quando os valores de a se aproximam de 3 pela direita, . Para esses valores:
para achar o limite esquerdo, ou seja, o limite quando os valores de a se aproximam de 3 pela esquerda, . Para esses valores:
O limite bilateral só existe se os limites laterais forem iguais. Como
Então,
Resposta
Exercícios de Livros Relacionados
Encontre o limite ou demonstre que ele não existe: lim x → ∞ 1 - e x 1 + 2 e x
Encontre o limite ou demonstre que ele não existe: lim x → ∞ ( e - x + 2 cos 3 x )
Encontre o limite ou demonstre que ele não existe: lim x → ∞ arctan ( e x )
Encontre o limite ou demonstre que ele não existe: lim x → ∞ x 4 - 3 x 2 + xx 3 - x + 2
Encontre o limite ou demonstre que ele não existe: lim x → ∞ [ ln 2 + x - ln ( 1 + x ) ]