Use o Método de Newton para aproximar, com duas casas decimais, as coordenadas dos pontos de inflexão da função:

Pra achar os pontos de inflexão, precisamos dos pontos onde essa função zera. Pra ser mais exato, precisamos dos pontos onde:

Vamos dar uma olhada no gráfico pra a gente poder saber onde mais ou menos está o ponto...

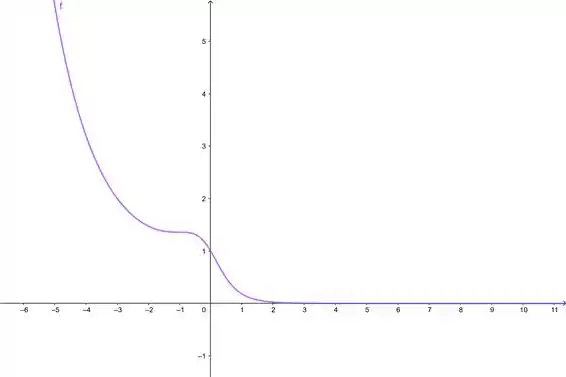
Pelo gráfico a gente vê que os pontos estão próximos de e . Vamos aproximar isso pelo método de Newton...

Para usar o método de Newton, a gente faz:

Vamos usar o primeiro.

Sendo que a nossa .

Vamos derivar:

E aplicar na fórmula:

Então o nosso primeiro ponto de inflexão tá ali, próximo do .

Ponto de inflexão:

Vamos ver o outro ponto de inflexão agora. Vamos usar . Teremos:

Vamos parar por aqui agora. Nosso outro ponto de inflexão então fica aproximadamente em:

Prontinho😊