Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.1 - Ex. 54
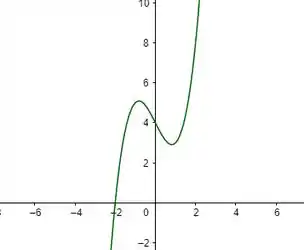
Determine os valores extremos (absoluto e local) das funções e onde ocorrem:
Passo 1
Sabendo que um ponto crítico é um valor extremo de uma função, a derivada da função deve ser igual a 0, uma vez que representa a inclinação de uma reta tangente que passa por esse ponto.
Encontrados os pontos críticos, calculamos a segunda derivada e igualamos a 0, para determinar se os pontos são de máximo ou mínimo.
Passo 2
Derivando a equação acima, teremos:
Passo 3
Para determinarmos os valores extremos, precisamos identificar os pontos críticos:
Passo 4
Substituindo na equação original, poderemos analisar quais pontos correspondem a mínimos e máximos.
Passo 5
Para classificarmos os pontos críticos, primeiro fazemos a segunda derivada e depois .
Quando o ponto da segunda derivada é 0, temos um ponto de inflexão. Dessa forma, analisamos os sinais de nossos pares ordenados para classificar o que é mínimo e máximo.
Passo 6
Agora que conhecemos os pares ordenados que correspondem aos pontos críticos, vamos classificá-los como mínimos e máximos globais e locais.
