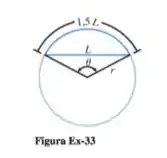
(a) Mostre que, sobre um círculo de raio o ângulo central que subentende um arco de comprimento 1,5 vezes o comprimento L de sua corda satisfaz a equação (ver Figura Ex-33).
(b) Use o Método de Newton para aproximar .
Passo 1
Fala aí! Tudo joia?
- Vamos chamar de o comprimento do arco e de o comprimento da corda.
- Vamos lá, a nossa função é onde aquela relação ali de cima zera. Ou seja:
Temos pela figura que certo?
Show! Agora a gente vai usar a relação que e .
E daí, a gente vai ter:
E prontinho! Provamos o que queríamos😉
Passo 2
Para usar o método de Newton, a gente faz:
Vamos derivar então:
Precisamos de um . Vamos começar com .
Vamos lá...
Passo 2
Então a aproximação do ângulo em radianos é aproximadamente . Em graus então é aproximadamente
Resposta
- Demonstração.