Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.7 - Ex. 28

Use o Método de Newton para aproximar o máximo absoluto de f x = x   s e n   x no intervalo 0 , π .

Passo 1

Fala aí! Tudo joia?

Pra começar aqui a gente tem que calcular esse ponto mínimo da função. A gente começa derivando a função. Fica assim:

f ' x =     s e n   x + x cos ⁡ x

A gente precisa de um ponto que zera isso, ou seja, um ponto em que:

s e n   x + x cos ⁡ x = 0

Passo 2

Vamos dar uma olhada no gráfico pra a gente saber onde mais ou menos onde está o nosso mínimo:

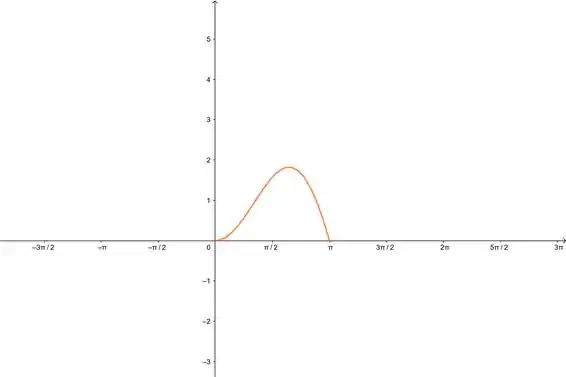
Nosso máximo tá ali, depois de x = π 2 . Pra usar o método de Newton, a gente precisa fazer:

x n + 1 = x n - g x n g ' x n

E vamos usar o x 1 = π 2 aí.

Passo 3

A nossa g x é a função que queremos zerar:

g x = s e n   x + x cos ⁡ x

Derivando, temos:

g ' x = cos ⁡ x + cos ⁡ x - x s e n   x

= 2 cos ⁡ x - x   s e n   x

Agora a gente aplica na fórmula:

x 2 = π 2 - s e n π 2 + π 2 cos ⁡ π 2 2 cos ⁡ π 2 - π 2 s e n π 2 = 2,207

x 3 = 2,036

x 4 = 2,029

Podemos parar por aqui, e concluímos que o nosso ponto máximo absoluto fica ali perto de x = 2,03 😉

E aí o valor máximo absoluto é aproximadamente f 2,03 =   1,82 .

Resposta

Ponto mínimo absoluto: ( 2,03 ,   1,82 ) .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y = x x 2 + 1
Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y = cos - 1 ⁡ ( x ² ) ²
Determine os pontos críticos,extremidades de domínio e valores extremos (absolutos e locais) da função: y = x 2 3 ( x + 2 )
Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y = e x + e - x
Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y = e x - e - x