Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.9 - Ex. 35a
- Use o método de Newton para encontrar os números críticos da função
corretos até a terceira casa decimal.
Passo 1
E aí, tudo certinho? 😊
O enunciado pede para encontarmos os números críticos (ou pontos críticos) da função
usando o método de Newton.
Os números críticos são os pontos do domínio em que ou não está definida, beleza? Mas e esse tal de método de Newton, você se lembra dele 🤔? Se liga só como ele funciona!
Para encontrar as raízes de uma equação , escolhemos um chute inicial , de preferência perto de uma das raízes, e a partir dele formamos uma sequência
e assim por diante:
Se essa sequência convergir, então o limite será uma raiz de .
Vamos usar esse método para resolver a equação e encontrar os números críticos da função . Para isso, vamos precisar:
- Encontrar a primeira derivada , pois queremos encontrar as suas raízes.
- Encontrar um bom candidato inicial a partir de um gráfico.
- Encontrar a segunda derivada para usarmos o método de Newton.
- Para cada raiz de calcular os termos da sequência e encontrar o valor procurado.
🚨 Fica esperto que a função do método de Newton é a derivada da função dada, combinado? Além disso, vamos precisar fazer algumas continhas. Uma calculadora pode te ajudar 😊!
Passo 2
Como a função é um polinômio, então para calcular a sua derivada vamos usar a Regra da Potência
em cada um dos seus termos.
Assim:
e como a função é um polinômio de grau , então ela vai ter até três raízes, né? Para cada uma das raízes, precisamos encontrar um bom chute inicial .
Espia só como faremos isso!
Passo 3
Para escolhermos um bom chute inicial para cada uma das raízes de
vamos usar uma ferramenta gráfica para obtermos o seu gráfico.
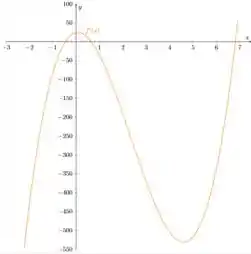
Analisando o gráfico, observe que a função possui três raízes, sendo uma no intervalo , outra no intervalo e mais uma em
Com isso, para cada raiz, temos como boas escolhas iniciais para :
Passo 4
Podemos obter bons chutes iniciais para sem plotar um gráfico. Para isso, precisamos analisar o sinal da função em alguns pontos. Saca só!
Em :
ou seja,
Em :
ou seja,
Em :
ou seja,
Consegue perceber que a função troca de sinal entre e e entre e ? Sendo assim, o Teorema do Valor Intermediário diz que exite uma raiz em e outra em ! Legal né?
Mas falta uma raiz. Perceba que a função é positiva no infinito (o único termo negativo é ). Logo, para algum valor maior do que ela deve voltar a ser positiva.
Em , temos que
e em temos
.
Opa, a função muda de sinal no interevalo , então ela tem uma raiz nele também.
Sabendo os intervalos onde as raízes estão, basta pegarmos um valor dentro de cada intervalo para ser o chute inicial de cada raiz.
Passo 5
Precisamos calcular a derivada que vamos usar para encontrar os termos da sequência do método de Newton.
Usando a Regra da Potência novamente, temos que a derivada de
é
Agora temos tudo o que precisamos para calcular os termos da sequência e estimarmos cada uma das raízes. Vamos lá!
Passo 6
A partir de agora, vamos usar a seguinte notação
e
Vamos começar obtendo a aproximação para a raiz que está no intervalo
Fazendo , então pelo método de Newton temos:
Como
e
então:
Agora, vamos calcular o terceiro termo !
Como
e
então:
Para o quarto termos , temos que como
e
então:
Observe que até a terceira casa decimal, então a raiz no intervalo é:
Passo 7
Vamos obter a aproximação para a raiz que está no intervalo
Fazendo , então pelo método de Newton temos
Como
e
Então:
Encontrando o terceiro termo !
Como
e
então:
Para o quarto termo , como
e
então:
Observe até a terceira casa decimal, então a raiz no intervalo é:
Passo 8
Vamos obter a aproximação para a raiz que está no intervalo
Fazendo , então pelo método de Newton temos:
Como
e
então:
Encontrando o terceiro termo !
Como
e
então:
Para o quarto termo , como
e
,
então
Observe até a terceira casa decimal, então a raiz no intervalo é:
Resposta
Os números críticos de são: