Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 24
Um recipiente de base quadrada, lados verticais e aberto em cima deve ser feito de de material. Encontre as dimensões do recipiente com maior volume.
Passo 1
Consideremos como o tamanho do lado da base quadrada e o tamanho das arestas verticais do recipiente. Uma figura ajuda a visualizar:
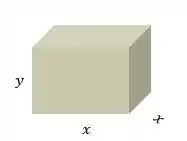
A expressão pro volume será:
Passo 2
Temos que a área total de material deve somar 90 metros quadrados. E a área total vai ser dada pela área da base somada com a área das 4 laterais.
Temos pra área da base :
E pra área das 4 laterais, , todas idênticas:
A expressão pra área total do recipiente é o somatório dessas duas expressões, que resulta em 90:
Passo 3
Agora vamos isolar dessa expressão de , pra podermos substituir na equação do volume e obtermos o volume em função apenas de . Teremos:
Reescrevemos a expressão do volume com essa sentença pra , e teremos pra :
Passo 4
Agora vamos derivar a função, igualar a derivada a zero e assim determinar os pontos críticos. Entre eles, os pontos de máximo e de mínimo. Aqui, nos interessa o ponto de máximo, que vai maximizar o volume.
Derivando:
Igualando a zero:
Nesse caso, só nos interessa o valor pois é um comprimento e não pode ter valor negativo. Esse será nosso ponto de máximo, logo, a dimensão que faz o recipiente ter o maior volume possível.
Precisamos ainda de , que obtemos facilmente com a expressão que já temos:
Resposta
São as dimensões e .