Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.8 - Ex. 18
Use o método de Newton para encontrar todas as raízes da equação com precisão de seis casas decimais.
Passo 1
Fala aí! tudo certinho?
Nesse problema foi pedido pra usarmos o método de Newton para encontrar as raízes da equação
Parece complicado?
Para resolver esse problema temos que transformar essa equação em uma função... pra isso passamos todos os termos para um lado e fazemos , ou seja
Já o método de Newton consiste em aplicar a fórmula
A partir de um chute inicial
Sacou? Bora começar!
Passo 2
Vamos começar calculando a derivada de ...
Nesse caso vamos aplicar a regrada potência e o Teorema Fundamental do Cálculo
Agora podemos aplicar a formula de Newton!
Veja só!
Passo 3
Pronto, agora que temos é só jogar na fórmula de Newton:
Vamos agora analisar qual valor usar para , pelo gráfico abaixo de e parece ter ponto de intersecção em , pronto, agora é só substituir, vamos lá então:
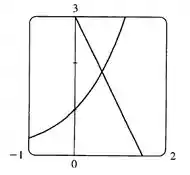
Como queremos uma precisão de seis casas decimais, vamos continuar usando o método de Newton até o valor de deixar de variar, vamos lá:
Mais uma vez, agora com :
Pronto, o valor não varia mais, então a raiz é .
E aí! entendeu tudo? Responde Aí!
Resposta
A raiz da equação é .