Use o método de Newton para encontrar todas as raízes da equação com precisão de seis casas decimais.

Para achar a derivada de vamos usar algumas regras de derivação, o da função constante, da cadeia, da função logaritmica e do polinômio:

Vamos calcular :

Vamos aplicar aqui então a regra da cadeia, iremos derivar a função e depois derivar quem chamamos de :

Pronto, agora que temos é só jogar na fórmula de Newton:

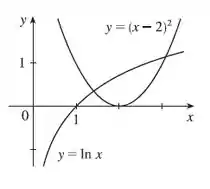
Vamos agora analisar qual valor usar para , pelo gráfico abaixo parace ter pontos de intersecção em e .

Mas veja, podemos utilizar nosso como qualquer valor, QUALQUER, mas é interessante analisar a função para que o nosso seja o mais próximo possível da raiz.

O gráfico é uma forma de nos ajudar a ser mais rápido, a gente plotou o gráfico utilizando o Desmos aqui para sermos práticos, você poderia ter feito um esboço rápido do gráfico para encontrar uma boa opção para o seu .

pronto, agora é só substituir, vamos lá então:

Assim, vamos fazer primeiro para e depois para .

Primeiro para :

Como queremos uma precisão de seis casas decimais, vamos continuar usando o método de Newton até o valor de deixar de variar, vamos lá:

Mais uma vez, agora com :

Vamos lá, uma hora acaba, agora :

Pronto, o valor não varia mais, então a raiz é .

Agora com , sei que é cansativo mas vamos lá:

Como queremos uma precisão de seis casas decimais, vamos continuar usando o método de Newton até o valor de deixar de variar, vamos lá:

Mais uma vez, agora com :

Vamos lá, uma hora acaba, agora :

Pronto, o valor não varia mais, então a raiz é .