Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.1 - Ex. 18
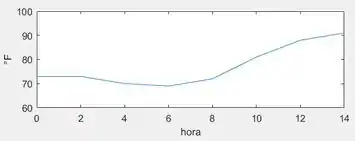
Os registros de temperatura foram tomados de duas em duas horas a partir da meia-noite até as horas, em Dallas, em de junho de. O tempo foi medido em horas após a meia-noite.
- Use os registros para esboçar um gráfico de como uma função de .
- Use seu gráfico para estimar a temperatura às horas da manhã.
Passo 1
Fala galerinha!
Essa questão nos dá uma tabela com valores de temperatura a cada 2 horas.
Primeiro temos que fazer um gráfico de em função de . Ou seja, a temperatura vai ser o nosso eixo das ordenadas e o tempo vai ser nosso eixo das abcissas.
Pra traçar esse gráfico, primeiro a gente precisa identificar os nossos pares ordenados, que tem a forma . Eles são:
Então pra fazer esse gráfico, é só marcar cada um desses pontos no plano cartesiano e depois ligar os pontos.
No item b, queremos estimar a temperatura às horas da manhã. Pra isso, vamos usar os pontos conhecidos mais próximos, um maior e um menor.
Passo 2
Então, como falamos no passo 1, vamos pegar os pares ordenados e marcar os pontinhos no plano cartesiano:
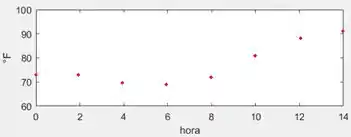
E agora é só ligar os pontos!
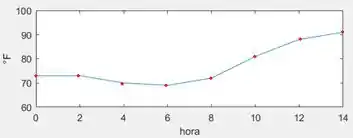
Essa gráfico, fizemos com o software Matlab.
Passo 3
Para estimarmos o valor da temperatura às horas da manhã basta pegarmos o valor menor e o maior.
E vamos considerar que a temperatura às seja a média aritmética entre eles:
Também podemos olhar pelo gráfico e obter um valor aproximado:
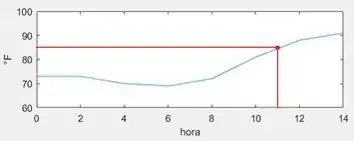
Resposta
