Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 11.6 - Ex. 22

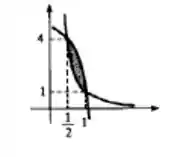
Desenhe o conjunto A dado e calcule a área:

A é o conjunto de todos (x, y) tais que x > 0 e 1 x 2 ≤ y ≤ 5 - 4 x ² .

Passo 1

Oi, pessoal! Nessa questão precisamos encontrar a área que está entre duas funções! Então vamos começar desenhando a função, para depois montar a integral e calcular.

Pelo enunciado temos que a área está entre y = 1 x 2 e y = 5 - 4 x 2 . Vamos ver onde essas curvas se cruzam?

1 x 2 = 5 - 4 x 2

1 = x 2 5 - 4 x 2

4 x 4 - 5 x 2 + 1 = 0

Resolvendo a equação vamos encontrar quatro raízes,

x 1 = - 1

x 2 = - 1 2

x 3 = + 1 2

x 4 = + 1

Como a questão pede a região onde x > 0 , as curvas se cruzam em

x = 1 2 e x = 1

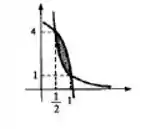
Passo 2

Pelo gráfico temos que a função maior é y = 5 - x 2 e a função menor é y = 1 x 2 . Logo a nossa integra será:

Á r e a = ∫ 1 2 1 5 - 4 x 2 - 1 x 2     d x = 5 x - 4 x 3 3 + 1 x 1 2 1 = 1 3

Resposta

Á r e a = 1 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a Parte 2 do Teorema Fundamental do Cálculo para calcular a integral, ou explique por que ela não existe. ∫ π 2 π c o s s e c 2 ( θ )d θ
Use a Parte 2 do Teorema Fundamental do Cálculo para calcular a integral, ou explique por que ela não existe. ∫ 0 1 x 4 5d x
Use a Parte 2 do Teorema Fundamental do Cálculo para calcular a integral, ou explique por que ela não existe. ∫ 1 4 1 xd x
Use a Parte 2 do Teorema Fundamental do Cálculo para calcular a integral, ou explique por que ela não existe. ∫ 0 1 3 + x xd x
Calcule a integral ∫ π 4 π 3 sec ⁡ θ t g θ d θ