Use um recurso gráfico computacional para determinar o número de vezes que as curvas se intersectam; aplique, então, o Método de Newton, quando necessário, para aproximar a coordenada de todas as interesecções.

e

Se temos:

Podemos arrumar esse cara:

Show, então queremos resolver essa equação. Podemos usar o Método de Newton para isso, em que:

Agora, para achar o nosso primeiro “chute” para o valor de , vamos olhar para o gráfico dessa equação e ver onde estão as raízes. O gráfico de é:

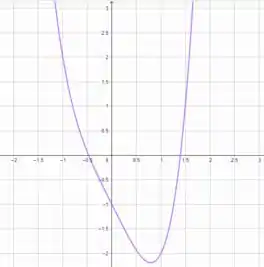
Olhando bem, podemos perceber que uma raiz está entre e (mais perto de ) e a outra entre e (mais perto de .

Primeiro, vamos ver se é solução:

Não é exatamente a raiz, mas chega bem perto. Usando Newton, vamos ver para onde a solução converge, usando e sabendo que e :

Continuando com o processo, usando uma calculadora:

Opa, devido à repetição dos valores, vemos que é uma aproximação para o primeiro valor.

Agora, vamos ver se é solução:

Não é exatamente a raiz, mas chega bem perto. Usando Newton, vamos ver para onde a solução converge, usando e sabendo que e :

Continuando com o processo:

Opa, devido à repetição dos valores, vemos que é uma aproximação para o segundo valor.

Então, nossas respostas serão:

E