Use um recurso gráfico computacional para estimar os valores máximo e mínimo absolutos de f , se houver, nos intervalos indicados e use os métodos do Cálculo para obter os valores exatos. f x = x - 1 2 x + 2 2 ; - ∞ ,+ ∞

Pontos de mínimo absoluto em x = - 2ex = 1 .Máximo relativo em x = - 1 2 Ponto de máximo absoluto não temos.

Enunciado

Oii tudo bem?

Mais uma de máximo e mínimo aí pra a gente!

Primeiro vamos ver usando um gráfico da função. Eu plotei no Geogebra e deu isso aqui oh:

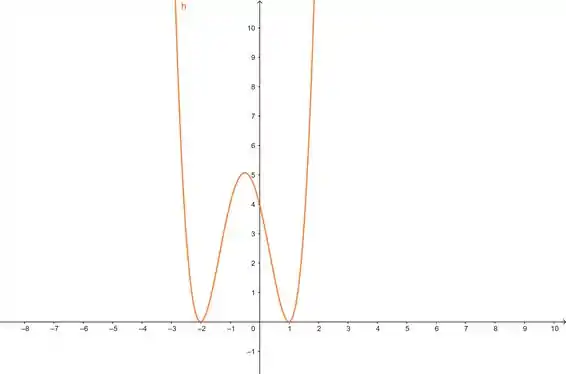
Então olha só, dois mínimos absolutos em e , um máximo relativo em (aproximadamente). Máximo absoluto a gente não tem!

Vamos fazer isso do jeito tradicional agora!

Pra derivar essa função a gente vai ter que usar regra do produto e da cadeia, então toma cuidado aqui:

Isso! agora a gente pode fazer isso aqui oh:

Vamos ver onde isso zera então. Pra zerar, algum dos fatores tem que ser zero.

Isso aí! Achamos os mesmos valores do gráfico! Daí era só testar pra saber qual que é mínimo ou máximo, mas a gente já sabe né😉

E prontinho! Conferiu com o que vimos no gráfico😉

Pontos de mínimo absoluto em .

Máximo relativo em

Ponto de máximo absoluto não temos.