Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.3 - Ex. 78
Onde a função periódica assume seus valores extremos, e que valores são esses?
Passo 1
Vamos começar derivando a função:
Os pontos críticos são quando a derivada é zero:
nunca ocorre, pois a exponencial é sempre maior ou igual a 1, então:
Que são os nossos pontos críticos.
Passo 2
Vamos testar agora o tipo de extremo que temos:
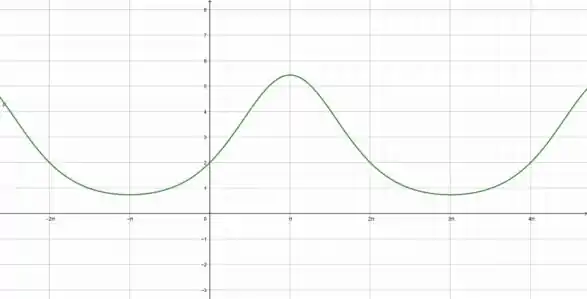
Então, temos um ponto máximo em , onde o valor é e um ponto mínimo em , onde o valor é , mas a função é periódica então o valor se repete a cada como podemos ver no gráfico:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Determinar o ponto A da curva y = x 2 + x que se encontra mais próximo de 7,0 . Mostrar que a reta que passa por 7,0 e por A é normal à curva dada em A .
Traçar uma tangente à elipse 2 x 2 + y 2 = 2 de modo que a área do triângulo que ela forma com os eixos coordenados positivos seja mínima. Obter as coordenadas do ponto de tangencia e a área mínima.
Uma pista de atletismo de comprimento total de 400m consiste de 2 semicírculos e dois segmentos retos, conforme figura a seguir. Determinar as dimensões da pista, de tal forma que a área retangular, d
Uma janela tem a forma de um retângulo encimado por um semicírculo. Achar as dimensões de modo que o perímetro seja 3,2m e a área seja a maior possível.
Duas industrias necessitam de água potável. A figura a seguir esquematiza a posição das indústrias, bem como a posição de um encanamento retilíneo l , já existente. Em que ponto do encanamento deve se