Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.3 - Ex. 63
Use um recurso gráfico para fazer estimativas grosseiras dos intervalos nos quais e os encontre exatamente por diferenciação.
Passo 1
Primeiro ele pede pra gente usar recursos gráficos, então vamos atender o pedido né?
O gráfico desse cara é:
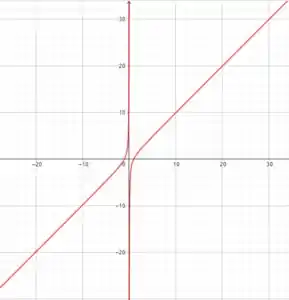
Bom, o que caracteriza a derivada da função em um ponto ser maior que zero? Se isso acontece, quer dizer que a função é crescente naquele ponto. Olhando pra esse gráfico, a gente pode perceber que a função não para de crescer em nenhum momento! Me diz um intervalo em que ela não cresca: não tem! Mas temos que olhar com mais cuidado também: perceba que no a função não toca, é uma assíntota vertical, por causa daquele na função. Opa, se a função não toca no e cresce em todo o resto, podemos dizer que:
A função possui para todo .
Passo 2
Como a gente consegue mostrar isso com diferenciação? Primeiro, vamos calcular a derivada dessa função:
Cara, olhando para essa derivada, vemos que o único termo com ali é o , só que qualquer número elevado ao quadrado é positivo e não temos nenhum termo negativo na função também. Então, não tem como essa derivada ser negativa, nem zero, ela sempre será positiva. Porém, olhando para o mesmo termo , vemos que, se , a função “explode”, ou seja, como vimos no passo anterior, é uma assíntota vertical nessa função. Logo, agora podemos dizer com certeza, pois calculamos de fato isso, que:
A função possui para todo .
Resposta
A função possui para todo .