Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.8 - Ex. 2a

Esboce os gráficos de f , f ' e f ' ' .

a) f (x) = x^2 |x|

Passo 1

Primeiramente, escrevemos a função em duas setenças, por causa do módulo:

f (x) = {[[x^2 (- x) , x < 0],[x^2 (x) , x >= 0]])

f ( x ) = {[[- x^3 , x < 0],[x^3 , x >= 0]])

E então, derivamos a função f (x) , setença por setença:

f^' = [f (x)]^' = {[[[- x^3]^' , x < 0],[[x^3]^' , x > 0]])

f^' = {[[- 3 x^2 , x < 0],[3 x^2 , x >= 0]])

Passo 2

Agora, derivamos f ' para obter f ' ' :

f^(' ') = [f^']^' = {[[[- 3 x^2]^' , x < 0],[[3 x^2]^' , x > 0]])

f^(' ') = {[[- 6 x , x < 0],[6 x , x >= 0]])

Passo 3

Agora vamos usar nossos resultados para esboçar a função f em vermelho, a primeira derivada f ' em azul e a segunda derivada f^(' ') em verde:

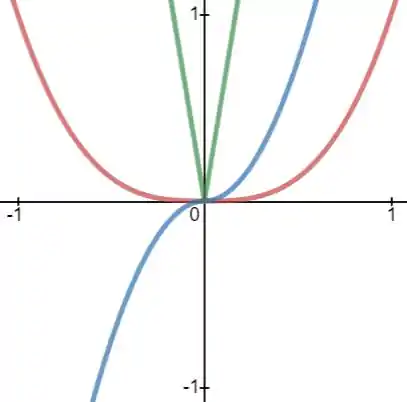
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Represente graficamente as curvas nos Exercícios 37-46Em que ponto os gráficos parecem ter tangentes verticais?Confirme as suas conclusões no item (a) com cálculos de limite. Mas, antes disso, leia a
Determine as equações de todas as retas com coeficiente angular - 1 que sejam tangentes à curva y = 1 / ( x - 1 ) .
Determine o coeficiente angular da tangente à curva y = 1 / x no ponto em que x = 4 .
Represente graficamente as curvas nos Exercícios 37-46Em que ponto os gráficos parecem ter tangentes verticais?Confirme as suas conclusões no item (a) com cálculos de limite. Mas, antes disso, leia a
Determine uma equação da reta que tenha coeficiente angular 1 / 4 e que seja tangente à curva y = x .