Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.1 - Ex. 41
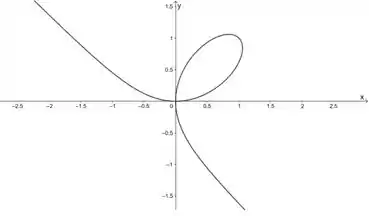
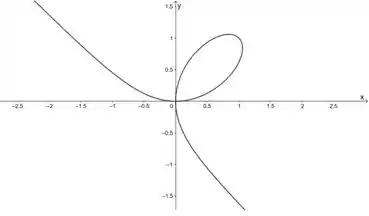
(a) Use o recurso de traçar gráficos implícitos de um CAS para esboçar o gráfico da curva cuja equação é .
(b) Use o gráfico de (a) para estimar a coordenada de um ponto do primeiro quadrante que está em e no qual a reta tangente a é paralela ao eixo .
(c) Encontre o valor exato da coordenada em (b).
Passo 1
(a) Vamos usar aqui a calculadora CAS do Geogebra (dá para acessar pelo navegador) para esboçar esse gráfico aí.
Colocando a equação do enunciado lá, temos esse gráfico aqui:
Passo 2
(b) Escolher um ponto onde a reta tangente é paralela ao eixo é o mesmo que escolher um ponto onde o gráfico da nossa função está mais na horizontal.
A gente pode escolher esse ponto aqui:
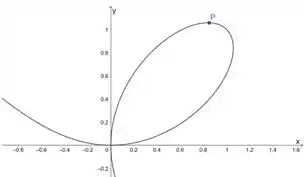
Onde:
Nossa estimativa é:
Passo 3
(c) Para estimar o valor exato da coordenada desse ponto, a gente vai precisar achar o valor de onde a reta tangente é paralela ao eixo .
Que é o mesmo que achar o ponto onde o coeficiente angular da reta é nulo:
E para achar precisamos derivar a nossa equação implicitamente.
Vamos lá!
Passo 4
Derivando nossa equação dos dois lados:
Como é uma função de , em temos um produto de funções e em temos uma função composta, por isso a gente precisa usar a regra do produto e a regra da cadeia:
Agora isolamos para achar :
Passo 5
Precisamos descobrir que resulta em :
Então nosso ponto está dentro dessa parábola, dentro da equação do enunciado e no primeiro quadrante. Vamos jogar na nossa equação:
Resolvendo para :
Como a gente quer a solução diferente de zero:
