Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 7.7 - Ex. 31

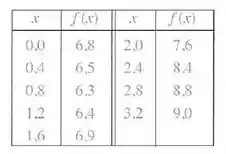
  1. Use a Regra do Trapézio e os dados a seguir para estimar o valor da integral ∫ 0 3,2 f x d x .

  2. Se soubermos que - 4 ≤ f ' x ≤ 1 para todo x , estime o erro envolvido na aproximação da parte (a).

Passo 1

  1. Temos os valores da função de 8 pontos de extremidade com comprimento 0,4 , o que nos dá um intervalo 0 ≤ x ≤ 8.0,4 ↔ 0 ≤ x ≤ 3,2 , e vamos usar n = 8 , temos que ∆ x :

    2. ∆ x = b - a n = 3,2 - 0 8 = 2 5

    Para achar a aproximação pela Regra do Trapézio fazemos uma média das aproximações da soma de Riemann, com a fórmula:

    T n = 1 2 ∆ x f x 0 + 2 f x 1 + 2 f x 2 + ∙ ∙ ∙ + 2 f x n - 1 + f x n

    T 8 = 1 2 ∆ x f 0 + 2 f 0,4 + 2 f 0,8 + 2 f 1,2 + 2 f 1,6 + 2 f 2,0 + 2 f 2,4 + 2 f 2,8 + f 3,2 = 1 2 ∙ 2 5 6,8 + 2.6,5 + 2.6,3 + 2.6,4 + 2.6,9 + 2.7,6 + 2.8,4 + 2.8,8 + 9,0 = 23,52

    Passo 2

  2. Para estimar o erro vamos usar as fórmulas dos erro na Regras do Trapézio:

E T ≤ K b - a 3 12 n 2

Se - 4 ≤ f ' x ≤ 1 temos que f ' ' x ≤ 4 , vamos então usar K = 4 e 0 ≤ x ≤ 3,2 .

Podemos pegar qualquer valor para K maior de 4 , mas o menor valor possível vai dar uma melhor estimativa para os erros. Temos n = 8 , a = 0 e b = 3,2 , vamos substituir na fórmula do erro então:

E T ≤ K b - a 3 12 n 2 ≤ 4 3,2 - 0 3 12 ∙ 8 2 ≈ 0,170666

Resposta

  1. T 8 = 23,52
  2. E T ≈ 0,170666
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o limite, reconhecendo primeiro a soma como uma soma de Riemann para uma função definida em 0,1 . lim n → ∞ ⁡ 1 n 1 n + 2 n + 3 n + … + n n
O gráfico da velocidade de um carro acelerado está mostrado a seguir.Dê uma estimativa da velocidade média do veículo durante os primeiros 12 segundos. Em que instante a velocidade instantânea foi igu