Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.5 - Ex. 10
(a) Encontre o valor médio de f no intervalo dado.
(b) Encontre c tal que .
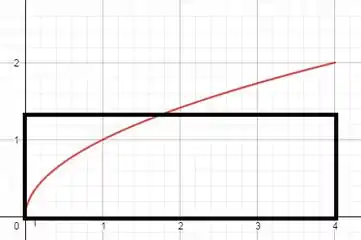
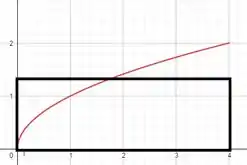
(c) Esboce o gráfico de f e um retângulo cuja área seja a mesma que a área sob o gráfico de f.
Passo 1
Muito bem, antes de começar vamos lembrar de como se calcula o valor médio da função, ok?
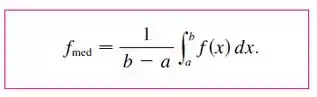
Tranquilo, não é?
Só vamos substituir:
Resolvendo:
Aplicando o intervalo:
Já conseguimos a letra a! Bora pra b!
Passo 2
Na letra b queremos um valor c, tal que a função seja igual a :
Vamos substituir c na função dada:
Vamos elevar ao quadrado para poder descobrir c:
Passo 3
Vamos desenhar a função dada pelo problema durante o intervalo, com x indo de 0 até 4.
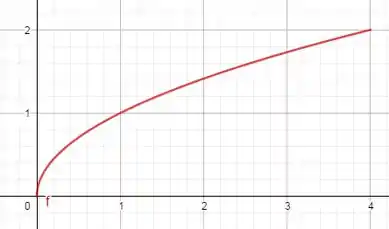
Qual a área abaixo do gráfico?
Basta integrarmos a função neste intervalo, não é?
Agora só precisamos fazer um retângulo cuja área também é 3. Se a área de um retângulo é dada por:
Então, podemos fazer um desenho cuja:
Desenhando:
