Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.5 - Ex. 1
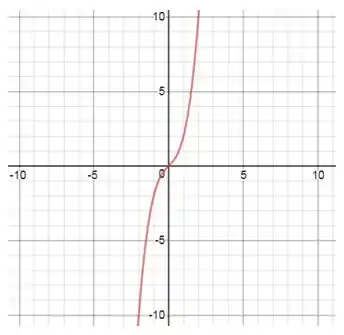
Use o roteiro dessa seção para esboçar a curva.
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
A questão pede para usarmos o roteiro de esboço de curvas dado na seção para esboçar o gráfico da função dada.
Para isso, devemos achar as raízes, intervalos de crescimento e decrescimento, máximos e mínimos, análise da concavidade e, daí, esboçar o gráfico.
Passo 2
Como se trata de um polinômio, o domínio é real: .
Passo 3
Vamos achar as interseções com os eixos e . Para o ponto que corta o eixo , basta tomar , assim o ponto onde isso ocorre é: .
Vemos então que a curva passa pela origem . Para as interseções com o eixo , fazemos , assim
A única raiz é pois não pode ser zero no conjunto dos reais. Assim, o único ponto de interseção com os eixos coordenados é .
Passo 4
Vamos ver se tem algum tipo de simetria trocando por :
Como , é uma função ímpar simétrica com relação à origem.
Passo 5
Como se trata de um polinômio, não tem assíntotas:
Passo 6
Para estudarmos os intervalos de crescimento e decrescimento, precisamos derivar :
Note que , de modo que , assim é estritamente crescente para todo real. Assim, a função não tem extremos locais nem globais.
Passo 7
Para a concavidade, precisamos da segunda derivada:
Assim,
O ponto é um ponto de inflexão.
Então abaixo nosso gráfico:
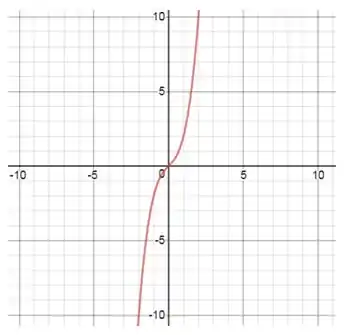
Resposta
Esboço da curva:
