Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.5 - Ex. 39
Use o roteiro desta seção para esboçar a curva.
Passo 1
Falaaa aeee, vamos para mais uma questão?
Nós temos a função
E aqui vamos seguir o seguinte roteiro para esboçar o gráfico dela.
A. Encontrar o domínio em que a função é definida.
B. Encontrar os interceptos. Que são os pontos onde a função cruza o eixo , isso é:
E o pontos onde a função cruza o eixo , isso é:
C. Verificar se há simetria par, isso é:
Para isso, basta substituir por e verificar se a expressão se mantém a mesma.
D. Procurar por assíntotas horizontais e verticais.
Uma assíntota horizontal é um valor real para o qual a função tende quando tende para infinito:
Já uma assíntota vertical é um valor de no qual a função possui uma descontinuidade e tende para infinito.
E. Encontrar os intervalos de crescimento e decrescimento. Para isso, basta derivar a função e nos intervalos em que a derivada for positiva a função cresce
E nos intervalos em que a derivada for negativa a função decresce
F. Encontrar os pontos de máximo e mínimo local.
Esses pontos ocorrem quando a derivada vale zero e troca de sinal ou quando a derivada possui uma descontinuidade e troca de sinal.
Caso a derivada fosse negativa e depois do ponto ela é positiva, então a função possui um ponto de mínimo local. Se a derivada era positiva e depois do ponto ela é negativa, então a função possui um ponto de máximo local.
G. Encontrar os intervalos de concavidade e pontos de inflexão.
A concavidade é para cima se a derivada segunda for positiva
E a concavidade é para baixo se a derivada segunda for negativa
Por fim, um ponto de inflexão é um ponto onde a derivada segunda vale zero e troca de sinal.
H. Esboçar a função juntando as informações obtidas.
Passo 2
Domínio
Nossa função não possui restrições em nenhum ponto, portanto seu domínio é o conjunto de números reais.
Passo 3
Intersecções com os eixos
No eixo , a intersecção ocorre quando
No eixo , temos:
Para que a exponencial valha zero é preciso que e como a função seno é definida entre e , isso nunca ocorrerá.
Portanto, a função não intercepta o eixo .
Passo 4
Simetria
Se fizermos
E
Sendo que a função é uma função par, portanto:
Dessa forma,temos:
E portanto, ficamos com:
Isso é, há simetria com relação ao eixo para a nossa função.
Passo 5
Assíntotas
Como a função não possui descontinuidade, não há assíntota vertical.
Para a assíntota horizontal fazemos:
No entanto, como a função seno é uma função periódica, ela não possui limite quando tende a infinito:
Dessa forma,
E portanto, a função não possui assíntota horizontal.
Passo 6
Intervalos de crescimento e decrescimento
Derivando a função, temos
O fator é sempre positivo.
Portanto, quem irá ditar se a derivada é positiva ou negativa será o cosseno.
Quando , temos
Isso nos dá e .
Dessa forma, cresce em e seus múltiplos, pois e
Já para o decrescimento, decresce em e seus múltiplos, pois e .
Passo 7
Valores de máximo e mínimo locais
O valor de máximo local ocorre quando e o valor de mínimo local ocorre em .
O valor da função nesses pontos é:
Esses valores se repetem a cada período de .
Passo 8
Concavidade e ponto de inflexão
Tirando a segunda derivada da função, temos
Aqui novamente, o fator sempre será positivo.
Para , temos
Concavidade para cima quando
Concavidade para baixo quando .
Pontos de inflexão quando
Passo 9
Esboço da curva
Podemos então esboçar graficamente a curva
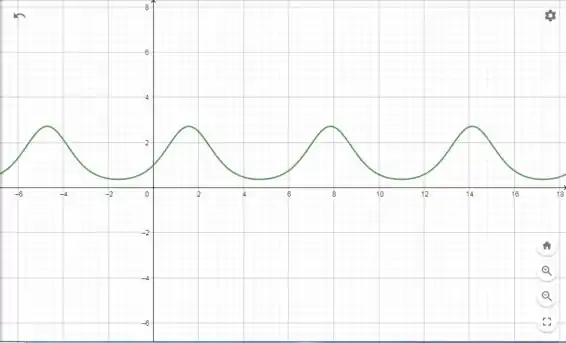
Resposta
