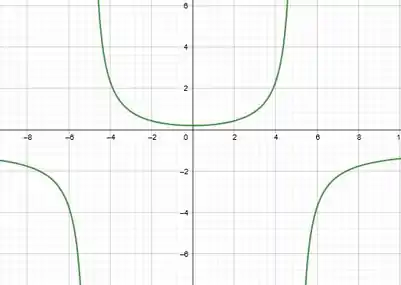
10. Use o roteiro desta seção para esboçar a curva:
Passo 1
Oiee, bora resolver mais uma comigo:
Para resolver essa questão necessitamos passar por alguns pontos da teoria
Domínio da função:
O domínio de uma função é o conjunto de todos os valores de para os quais a função está definida.
Para a função dada, devemos excluir os valores de que tornam o denominador igual a zero, pois a divisão por zero não é definida.
Portanto, o domínio é todos os números reais exceto
Interseções com os eixos:
As interseções da função com os eixos nos fornecem pontos importantes para esboçar o gráfico da função. Para encontrar as interseções com o eixo igualamos a zero e resolvemos para
Para a interseção com o eixo substituímos por zero na função.
Simetrias:
Uma função é simétrica em relação ao eixo se substituir por na função não altera seu valor.
Isso significa que a função é simétrica se for uma função par.
Assíntotas:
As assíntotas são linhas que a função se aproxima à medida que se aproxima de infinito ou menos infinito.
Podem ser verticais, horizontais ou oblíquas. Para encontrar assíntotas verticais, procuramos os valores de que tornam o denominador da função igual a zero.
Para assíntotas horizontais, observamos o comportamento da função quando tende a infinito ou menos infinito.
Comportamento para
Determinamos o comportamento da função quando se aproxima de infinito e menos infinito. Isso nos ajuda a entender como o gráfico se estende para a direita e para a esquerda.
Concavidade e pontos de inflexão:
A concavidade de uma função nos diz se ela está voltada para cima ou para baixo em diferentes partes do seu domínio.
Os pontos de inflexão são os pontos onde a concavidade da função muda.
Então, vamos seguir a seguinte sequência:
1. Determinar o domínio da função.
2. Encontrar as interseções da função com os eixos
3. Verificar se a função é simétrica em relação ao eixo
4. Encontrar as assíntotas verticais e horizontais, se existirem.
5. Determinar o comportamento da função para
6. Identificar a concavidade da função e possíveis pontos de inflexão.
7. Esboçar o gráfico da função com base nas informações obtidas nos passos anteriores.
Passo 2
O primeiro passo é definir o domínio de , isto é, o conjunto dos valores de para os quais está definida.
Temos neste caso que o denominador não é definido se for igual a zero, então podemos escrever que:
Assim, temos que:
Passo 3
Agora devemos definir as intersecções com os eixos. Para o eixo a interseção é dada por e para o eixo fazemos e isolamos o .
Assim, temos que:
E agora para :
E como não existe raiz de um número negativo, quer dizer que não existe.
Passo 4
Devemos verificar se a função possui simetria. Temos três casos:
- Se para todo em , é uma função par e a curva é simétrica em relação ao eixo . Caso isso ocorra basta refletir a curva em torno do eixo para obter a curva completa.
- Se para todo em , é uma função ímpar e é simétrica em relação à origem. Caso isso ocorra basta girar a curva em em torno da origem para obter a curva completa.
- Se para todo em , onde é uma constante positiva, é uma função periódica e o menor desses números é chamado de período. Caso isso ocorra pode-se usar a translação de um período para esboçar o gráfico inteiro.
Para esta função, tomando :
- Não possui período.
Logo, como a função satisfaz a propriedade (a), quer dizer que temos uma simetria em relação ao eixo y.
Passo 5
Devemos verificar agora se a função possui assíntotas:
- Assíntota horizontal:
- Assíntota vertical: a reta é uma assíntota vertical se pelo menos uma das seguintes afirmativas for verdadeira:
Se então a reta é uma assíntota horizontal da curva .
Se resultar que , então não temos uma assíntota à direita.
Temos:
Assim, temos uma assíntota horizontal em .
E como vimos em , nossa função não está definida então quer dizer que nesses pontos temos assíntotas verticais.
Passo 6
O próximo passo é definir os intervalos de crescimento ou decrescimento da função.
Calculamos e encontramos os intervalos nos quais é positiva ( é crescente) e os intervalos nos quais é negativa ( é decrescente).
Aplicando a regra do quociente na função , temos:
E igualando a zero temos que
Logo, é crescente para e decrescente em . E além disso temos que para , não existe, o que faz deles pontos críticos da função.
Passo 7
Calcularemos agora a concavidade da função utilizando . Se a função é côncava para cima e se a função é côncava para baixo.
Assim temos que:
E agora igualando a zero, temos
Logo, isso só é possível para .
Portanto a função é côncava para cima em
E côncava para baixo em:
Passo 8
Agora que temos todas essas informações, podemos esboçar o gráfico de , fica desse jeitinho ó:
Dado que temos todos os dados necessários, vou esboçar o gráfico da função
Domínio: Todos os números reais exceto
- Interseção com o eixo
- Assíntotas verticais:
- Comportamento para : A função se aproxima de zero.
- Não há pontos de inflexão ou assíntotas horizontais.
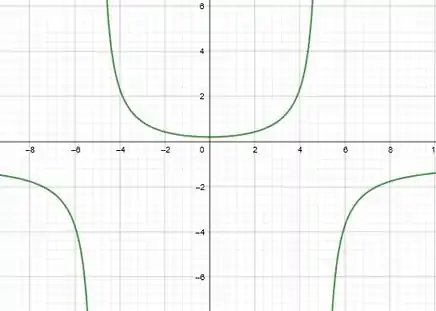
Resposta