Se é uma função positiva e para , mostre que

Vamos lá, como as aproximações do Trapézio e do Ponto Médio no intervalo são as somas das aproximações do Trapézio e do Ponto Médio nos subintervalos , onde , nós podemos focar em apenas um desses subintervalos.

A condição para significa que o gráfico é côncavo para baixo, como na figura abaixo:

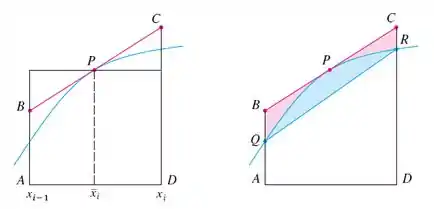
Nela, é a área dp trapézio , é a área da região , e é a área do trapézio , assim,

Temos em geral, que a condição implica que o gráfico de em encontra-se acima do local unindo os pontos e . Assim, .

Como é a área abaixo da tangente do gráfico, e como , implica que a tangente encontra-se acima do gráfico, assim vamos ter .

Assim, temos que: