67 – a) Use um SAC para calcular:

onde n é um número inteiro positivo arbitrário. O seu SAC pode determinar o resultado?

b) Em seguida, defina a integral quando n = 1, 2, 3, 5 e 7. Comente a complexidade dos resultados.

c) Agora substituía e some a nova integral com a antiga. Qual será o valor de:

Este exercício ilustra como uma pequena engenhosidade matemática resolve um problema que não pode ser solucionado imediatamente por um SAC.

Resolveremos o item C, utilizando o software Maple.

- Criaremos um novo arquivo em modo folha de trabalho, seguindo os passos:

Arquivo > Novo > Modo Folha de Trabalho

Pronto agora utilizaremos o software para realizar o exercício solicitado.

Utilizaremos o seguinte comando:

Por parte, cada expressão tem um significado no campo da programação:

q* (Apenas um nome qualquer atribuído para a expressão, pode ser inserido qualquer nome neste trecho);

≔ Expressão de programação que significa recebe;

Int() = Integral de um número.

ln = logaritmo natural;

/ Significa divisão ou fração;

^ - Signfica elevado em uma expressão matemática;

=value (q*) – Retorne o valor da expressão (insira o nome da expressão que deseja a resposta);

Simplify = comando para simplificar uma expressão.

Logo:

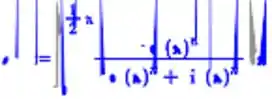
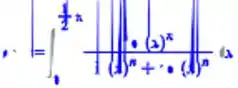
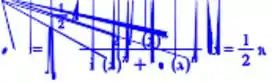
Assim obteremos o resultado da expressão !