Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 60
- Se
Use um sistema de computação algébrica para encontrar uma expressão para .
- Use a expressão da parte (a) para fazer na mesma tela um gráfico de , e .
Use um sistema de computação algébrica para encontrar uma expressão para .
Passo 1
Falaa... tudo bem??
Nessa questão foi dada a função:
E vamos usar algum programa pra encontrar a expressão para a inversa .
É só jogar no programa e pedir pela inversa mesmo.
Depois vamos plotar numa mesma tela os gráficos de , e .
Passo 2
-
Utilizando o Derive, podemos encontrar
Onde
E
Porém, como
Então esta expressão da função inversa só está definida no intervalo
O software Mapple nos dá o restante da solução
Onde
E está definida no intervalo
Passo 2
- Esboçando em um software, ficamos com
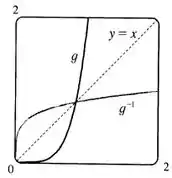
Repara que ele não pediu o esboço dessas curvas a toa.
Podemos notar que o gráfico da fun��ão inversa é o gráfico da função, espelhado em relação à reta
Resposta
Onde
Exercícios de Livros Relacionados
Determine expressões mais simples para as quantidades nos Exercícios 43-46.45. c) ln ( e - x 2 - y 2 )
Nos Exercícios 53 e 54, resolva em k .54. c) e^((ln 0,8) k) = 0,8
Nos Exercícios 47-52, resolva y em função de t ou x , conforme for apropriado.47. ln y = 2 t + 4
Use as propriedades dos logaritmos para simplificar as expressões nos Exercícios 41 e 42.42. c) 3 ln t 2 - 1 3 - l n ( t + 1 )
Determine expressões mais simples para as quantidades nos Exercícios 43-46.44. a) e l n ( x 2 + y 2 )