Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.4 - Ex. 37
(a) Como está definida a função logarítmica ?
(b) Qual o domínio dessa função?
(c) Qual é a imagem dessa função?
(d) Esboce a forma geral do gráfico da função se .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente explicar a definição da função logarítmica , determinar o domínio e a imagem dessa função e esboçar seu gráfico, sabendo que .
Então, vamos dar uma olhadinha na definição de função logarítmica e determinar seu domínio com base nos valores que pode assumir. Dessa forma, sua imagem serão os valores correspondentes. E depois vamos plotar isso no plano cartesiano.
Vamos lá!
Passo 2
Bom, vamos para a explicação do que é uma função logarítmica. A função logarítmica é também a função inversa da função exponencial de base . Então, temos a relação de equivalência:
Analisando os valores de que a função pode assumir, percebemos que não pode ser negativo quando o valor de for par. Como temos essa condição, excluímos os valores negativos de do nosso domínio.
Além disso, nenhum número elevado a alguma potência é zero, então também não pode ser zero. Dessa forma, nosso domínio será o intervalo aberto:
Mas para todos os valores de nesse domínio, nossa função tem um valor correspondente em , que pode ser qualquer número real. Sendo assim, sua imagem pertence ao conjunto , porque todo valor real pode ser escrito como um logaritmo.
Passo 3
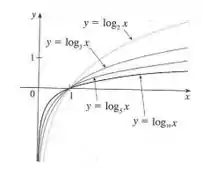
Agora, vamos desenhar o gráfico da função. Como pode ser qualquer número maior do que , podemos ter várias curvas. Olha só:
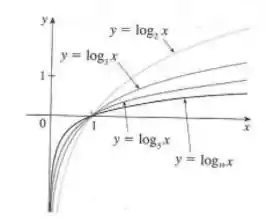
Valeu, galera! Até a próxima! 😉
Resposta
-
y = log a x - Domínio:
- Imagem:
