Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 7.4 - Ex. 4

Escreva as formas de decomposição em frações parciais da função (como no exemplo 7). Não determine os valores numéricos dos coeficientes.

  1. ∫ x 4 - 2 x 3 + x 2 + 2 x - 1 x 2 + 2 x + 1   d x
  2. ∫ x 2 - 1   x 3 + x 2 + x     d x  

Passo 1

Opa! Bora pra mais uma?!

Aqui o enunciado quer que a gente escreva as formas de decomposição em frações parciais das funções.

  1. ∫ x 4 - 2 x 3 + x 2 + 2 x - 1 x 2 + 2 x + 1   d x
  2. ∫ x 2 - 1   x 3 + x 2 + x     d x  

Ou seja, o enunciado quer que a gente pegue cada integral e “divida” ela em várias outras integrais usando frações parciais! Vamos ver como podemos fazer isso!

Passo 2

Vamos pra letra (a):

∫ x 4 - 2 x 3 + x 2 + 2 x - 1 x 2 + 2 x + 1   d x

A gente pode perceber que o numerador tem grau maior que o denominador, então dá pra simplificar aí! Bora dividir o numerador pelo denominador:

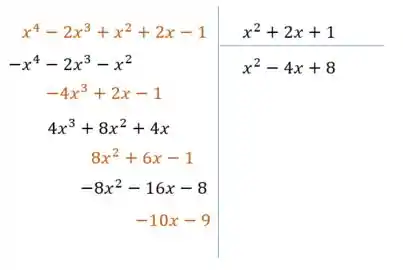
Temos então que:

x 4 - 2 x 3 + x 2 + 2 x - 1 = x 2 + 2 x + 1 x 2 - 4 x + 8 - 10 x + 9

Logo:

Agora olhando o numerador a gente pode tentar encontrar alguma coisa parecida:

x 4 - 2 x 3 + x 2 + 2 x - 1 x 2 + 2 x + 1 = x 2 - 4 x + 8 - 10 x + 9 x 2 + 2 x + 1

Note que precisamos reescrever o denominador em termos de grau menor apenas, já que agora o grau do numerador é menor que o do denominador :

x 2 - 4 x + 8 - 10 x + 9     x 2 + 2 x + 1   =   x 2 - 4 x + 8 -   10 x + 9     x + 1 2

Passo 3

Aqui é só separar cada termo do denominador da função no denominador de uma fração e coloca a constante no numerador:

x 2 - 4 x + 8 -   10 x + 9     x + 1 2 =     x 2 - 4 x + 8 -   A x + B x + 1 2 - D x + E x + 1

Temos então:

∫ x 4 - 2 x 3 + x 2 + 2 x - 1 x 2 + 2 x + 1   d x = ∫ x 2 - 4 x + 8 -   A x + B x + 1 2 - D x + E x + 1   d x

Passo 4

Na letra b, vamos reescrever o denominador em termos de grau menor apenas, já que o grau do numerador é menor que o do denominador:

x 2 - 1   x 3 + x 2 + x   = x 2 - 1 x x 2 + x + 1

Agora é só separar cada termo do denominador da função no denominador de uma fra��ão e coloca a constante no numerador, conforme as regrinhas do livro:

x 2 - 1 x x 2 + 1 = A x + B x + C x 2 + x + 1  

Finalmente:

∫ x 2 - 1   x 3 + x 2 + x     d x   = ∫ A x + B x + C x 2 + x + 1     d x  

Resposta

∫ x 4 - 2 x 3 + x 2 + 2 x - 1 x 2 + 2 x + 1   d x = ∫ x 2 - 4 x + 8 -   A x + B x + 1 2 - D x + E x + 1   d x

∫ x 2 - 1   x 3 + x 2 + x     d x   = ∫ A x + B x + C x 2 + x + 1     d x  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral. ∫ x 5 - 4 x 3 + 1 x 3 - 4 x d x
Calcule a integral. ∫ 2 x 2 + 3 x x - 1 2 d x
Calcule a integral. ∫ 10 ( x - 1 ) ( x 2 + 9 ) d x
Escreva as formas de decomposição em frações parciais da função (como no exemplo 7). Não determine os valores numéricos dos coeficientes. ∫ x 4 - 2 x 3 + x 2 + 2 x - 1 x 2 - 2 x + 1d x ∫ x 2 - 1x 3 +
Calcule a integral. ∫ a x x 2 - b x d x