Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.5 - Ex. 18

Esboce o gráfico.

f ( x ) = (x^2)/(x^2 - x - 2)

Passo 1

Se x estiver no domínio da função, então:

x^2 - x - 2 != 0 => x != - 1 e x != 2

Vamos derivar para achar os intervalos de crescimento e decrescimento:

f^' (x) = (2 x (x^2 - x - 2) - x^2 (2 x - 1))/((x^2 - x - 2)^2) = (- x^2 - 4 x)/((x^2 - x - 2)^2) = (- x (x + 4))/((x^2 - x - 2)^2)

Sendo assim, teremos crescimento quando f ' ( x ) > 0 , ou seja:

- 4 < x < 0

E decrescimento quando:

x < - 4 ou x > 0

Desse modo, x = - 4 corresponderá a um ponto de mínimo local e x = 0 a um ponto de máximo local.

Passo 2

Para estudar a concavidade, vamos derivar novamente:

f^(' ') (x) = (2 (x^3 + 6 x^2 + 4))/((x^2 - x - 2)^3)

Sendo assim, teremos concavidade para cima quando f^(' ') (x) > 0 , ou seja:

- 6,1 < x < - 1 ou x > 2

E concavidade para baixo quando:

x < - 6,1 ou - 1 < x < 2

Desse modo, x tildetilde - 6,1 é ponto de inflexão.

Passo 3

Agora vamos buscar assíntotas horizontais, calculando os seguintes limites:

underset(x -> +- oo)(lim) f (x) = underset(x -> +- oo)(lim) (x^2)/(x^2 - x - 2) = 1

Ou seja, nos dois extremos do domínio teremos retas assíntotas horizontais y = 1 .

Como x = - 1 e x = 2 não pertencem ao domínio da função, vamos calcular os seguintes limites laterais, a fim de achar assíntotas verticais:

underset(x -> - 1^+)(lim) f (x) = underset(x -> - 1^+)(lim) (x^2)/(x^2 - x - 2) = - oo

underset(x -> - 1^-)(lim) f (x) = underset(x -> - 1^-)(lim) (x^2)/(x^2 - x - 2) = + oo

underset(x -> 2^+)(lim) f (x) = underset(x -> 2^+)(lim) (x^2)/(x^2 - x - 2) = + oo

underset(x -> 2^-)(lim) f (x) = underset(x -> 2^-)(lim) (x^2)/(x^2 - x - 2) = - oo

Desse modo, temos assíntotas verticais x = - 1 e x = 2 .

Passo 4

Agora sim já temos um bocado de informação sobre o gráfico da função. Bora fazer o esboço?

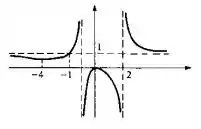
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Represente graficamente a equação seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflex
Represente graficamente a equação seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflex
Represente graficamente a equação seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflex
Suponhamos que a derivada da função y = f ( x ) seja y ' = x - 1 2 ( x - 2 ) ( x - 4 ) .Em que pontos, se houver, o gráfico de f apresenta um mínimo local, um máximo local, ou um ponto de inflexão?
Determine os valores das constantes a ,b e c , de modo que o gráfico de y = a x 3 + b x 2 + c x tenha um máximo local em x = 3 , um mínimo local em x = - 1 e um ponto de inflexão em ( 1 ,11 ) .