Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 20
Estime o valor do limite (se existir) pela avaliação da função nos números dados (usar 6 casas decimais).
Passo 1
Falaaa, pessoal. Tudo bem??
Nessa questão vamos estimar o valor do limite, se existir:
A partir dos dados:
Lembra que quando falamos de limite de tendendo a , falamos do valor da função quando está beeeem próximo de , certo? E é isso que vamos fazer na prática nessa questão.
Vamos usar valores que vão se aproximando de pela direita:
E valores que vão se aproximando de pela esquerda:
Para calcular a função que está dentro do limite para todos esses valores.
Se os limites laterais (de tentende a pela esquerda e de tendendo a pela direita) forem iguais a um número finito (não pode ser infinito ou menos infinito), dizemos que o limite existe e é igual ao valor desses limites.
Maaas se os limites laterais forem diferentes (ou se os dois forem infinito ou menos infinito), dizemos que o limite não existe.
Passo 2
Usando uma calculadora pra calcular a função:
Podemos montar as tabelas:
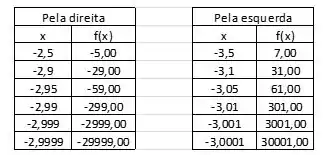
Repara que conforme vai se aproximando de pela direita, os valores de só vão diminuindo muuuuito. Vai ficando cada vez mais negativo, então dizemos que o limite lateral (pela direita):
E conforme vai se aproximando de pela esquerda, os valores de vão aumentando muuuuito. Então dizemos que o limite lateral (pela esquerda):
Portanto, o limite não existe.