Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 27
Use uma tabela de valores para estimar o valor do limite. Caso tenha um dispositivo de gráficos, usar para confirmar o resultado.
Passo 1
Faala meu consagrado
Para existir o limite, a função deve tender a um certo valor tanto pela esquerda quanto pela direita.
Nessa questão temos o seguinte limite:
Esse é um limite lateral pela direita. Ou seja, só precisamos ver o comportamento da função para valores maiores que .
Dessa forma, vamos aplicar valores de maiores que para ver seu comportamento pela direita.Por fim, vamos usar um recurso gráfico para plotar a função e verificar se os nossos resultados batem com o gráfico.
Passo 2
Vamos então usar a calculadora com valores próximos ao limite, apenas pela direita, para confirmar ou não esta tendência.
Ou seja, vou aplicar valores de na função que sejam maiores que , porém próximos de .
Por exemplo, com , obtenho o seguinte resultado.
Fazendo isso para diversos valores, obtemos a seguinte tabela:
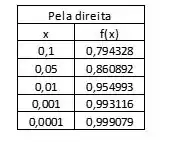
Vemos então que a tendência do limite pela direita é igual a
Passo 3
Fazendo o gráfico da função obtemos:
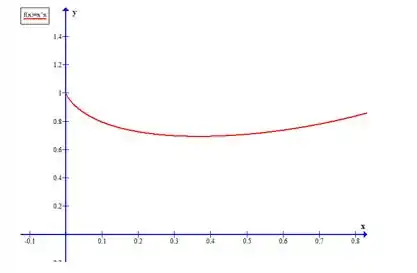
Dessa forma, vemos que quando tende a pela direita, a função tende a .O que confirma o nosso limite: