Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.2 - Ex. 23
Use uma tabela de valores para estimar o valor do limite. Se você tiver alguma ferramenta gráfica, use-a para confirmar seu resultado.
Passo 1
Eaeee, belezinha?? Bom... a questão nos dá o seguinte limite:
O enunciado quer que utilizemos uma tabela de valores para estimar o valor do limite.
Em outras palavras temos que ir aproximando a valores próximos de zero, tanto pelos números maiores quanto pelos números menores que zero.
Nessa brincadeira a gente está utilizando os limites laterais, em que um limite existe se o limite dos números de que aproximam-se pela esquerda forem iguais ao limite dos números de que se aproximam pela direita!!
Agora que a gente já sabe o conceito vamos lá!! 😉
Passo 2
Seja:
Construindo uma tabela com valores de tendendo a zero (aplicando o conceito dos limites laterais visto no Passo 1), ficamos com:
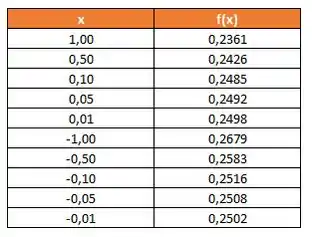
Pela tabela, podemos ver que
Já que os limites laterais são iguais, dizemos que o limite existe e vale:
Passo 3
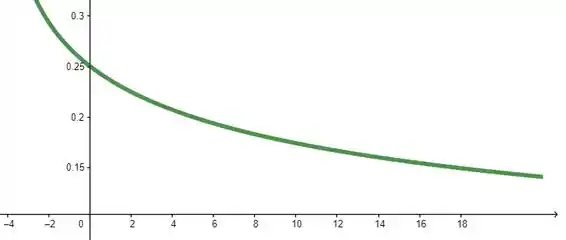
Pegando essa função bacana e jogando num plotador de gráficos:
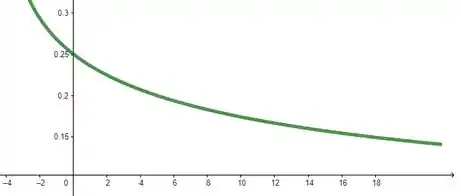
Dá pra ver que, de fato, essa função tende a quando tendemos a .
Entendeu direitinho?? Responde aee 😉
Resposta
