Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.8 - Ex. 39
Use o teorema 10.8.1 para achar a equação polar de uma cônica central cujo centro está na origem, o eixo principal está ao longo do eixo polar e de sua extensão e a distância da origem à diretriz é .
Passo 1
Sabendo que é qualquer ponto sobre a cônica, se desenharmos essa mesma cônica em um plano cartesiano, teremos o seguinte, pessoal:
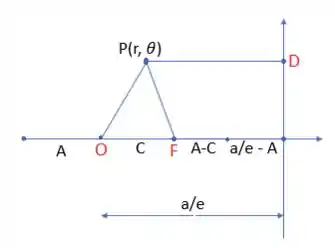
No qual as letras em vermelho são aqueles pontinhos específicos e as letras em preto são os tamanhos das retas, tudo bem? Uma das formas mais interessantes de determinarmos uma equação polar da cônica central que desenhamos, é utilizando a lei dos cossenos no triângulo . Sendo assim, teremos:
Aqui não tem mistério, não é mesmo galera? é a base do triângulo e é o comprimento esquerdo . No entanto, temos que descobrir e em função de e que são as variáveis da nossa equação polar, e é aqui que começa a resolução de fato!
Passo 2
Se observarmos com cuidado a figura do passo 1 segundo o teorema 10.8.1, notaremos que . Ademais, para descobrirmos e vamos criar um sisteminha, saca só:
Somando essas duas equações, obteremos:
Substituindo em qualquer uma das equações, teremos:
Agora que encontramos e em função de e , basta substituirmos lá na lei dos cossenos que escrevemos no passo 1 e pronto!
Passo 3
Substituindo e , teremos:
Ademais, utilizando um pouco de trigonometria, temos que , considerando que seja equidistante à e . Agora que temos tudo que precisamos, basta utilizarmos a seguinte expressão: