Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.2 - Ex. 34
O arco de uma ponte tem a forma de uma semi-elipse com um vão horizontal de 40 m e com 16 m de altura no centro. Qual a altura do arco a 9 m à esquerda ou à direita do centro?
Passo 1
Com os dados do enunciado podemos fazer a seguinte representação gráfica
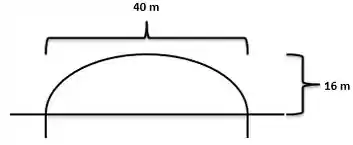
Assim temos que e , que assim encontramos os semi-eixos dessa elipse que são e .
Passo 2
Agora vamos montar a equação da elipse, tomaremos como origem o centro da elipse.
Passo 3
Vamos aplicar na elipse e encontrarmos que nos dará a altura do arco.
Vamos achar o M.M.C. desta divisão
Vamos por o em evidência
Como estamos trabalhando com distância somente o valor positivo vale
Resposta
Exercícios de Livros Relacionados
Determine as retas tangentes á elipse E que são paralelas à reta s . aE : 4 x 2 + 2 y 2 = 1 , s : y = 2 x bE : x 2 p + y 2 q = 1 , s : y = m x
Quais são os pontos da elipse E : x 2 a 2 + y 2 b 2 = 1 em que a reta normal contém a o centro? b um foco?
Mostre que a regra prática para se obter uma equação da reta tangente no ponto T = h , k não exige que a equação da elipse esteja na forma reduzida: é suficiente que ela contenha apenas termos em x 2e
Se F 1 e F 2 são os focos da elipse E : x 2 a 2 + y 2 b 2 = 1 , prove que: a P é um ponto interior a E se, e somente se, d P 1 F 1 + d P 1 F 22 a ; b P é exterior à elipse se, e somente, se d P 1 F 1
Determine as retas tangentes á elipse E : x 2 + 3 y 2 = 7 que contêm o ponto P = ( - 1 , - 3 ) .