Use o Teorema 5.4.2 para calcular as somas e verifique suas respostas usando um recurso computacional.
Passo 1
O teorema citado dá uma certa fórmula para calcular alguns tipos de somatório. Segundo ele, esse somatório da questão é calculado fazendo:
Nesse caso aqui a gente vai ter que dar uma mexidinha antes de aplicar. Vamos separar a soma:
E vamos jogar essa constante pra fora:
Show! Agora a gente joga no teorema...
Passo 2
Aquela primeira fica:
Juntando a constante multiplicativa:
A outra agora é de boa:
Agora a gente soma as duas:
Show! Calculamos o somatório!
Vamos verificar na calculadora do site :
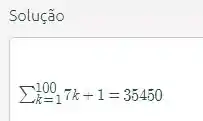
Certinho!