Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.2 - Ex. 60

( a ) Use um recurso gráfico computacional para gerar um campo de direções da equação diferencial d y / d x = e x / 2   na região - 1 ≤ x ≤ 4 e - 1 ≤ y ≤ 4 .

( b ) Esboce algumas curvas integrais representativas da função f x = e x / 2 .

( c ) Encontre uma equação para a curva integral que passa pelo ponto ( 0 ,   1 ) .

Passo 1

Bom galera, vamos começar gerando um campo de direções para a equação diferencial d y / d x = e x / 2 :

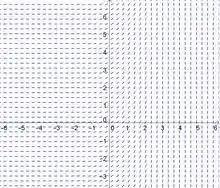
Passo 2

Agora, esboçamos o gráfico de algumas curvas integrais para a função f x = e x / 2 , lembrando que a integração vai gerar uma constante de desconhecida que muda a altura da função:

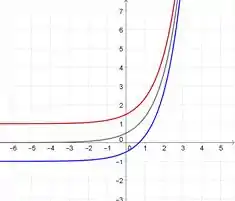
Passo 3

Por fim, a gente usa o problema de valor inicial para a integral de x :

∫ e x 2   d x = e x 2 + C

Agora olhamos testamos qual o valor de C para que a função passe pelo ponto ( 0 ,   1 ) :

f 0 = 1 = e ( 0 ) 2 + C

→ C = 1 2

Logo, a função fica:

f x = e x 2 + 1 2

Resposta

f x = e x 2 + 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use um sistema de computação algébrica para calcular a integral. Calcule a resposta com o resultado usando tabelas. Se as respostas forem diferentes, mostre que são equivalentes. ∫ x 2 x 2 + 4 ⁡ xd x
Use um sistema de computação algébrica para calcular a integral. Compare a resposta com o resultado usando as tabelas. Se as respostas forem diferentes, mostre que elas são equivalentes. ∫ x 2 1 - x 2
10. Deduza as seguintes Leis dos Logaritimos a partir de (15):a) log a ⁡ x y = log a ⁡ x + log a ⁡ y b) log a ⁡ x / y = log a ⁡ x - log a ⁡ y c) log a ⁡ x y = y log a ⁡ x
8. Prove a Segunda Lei dos Expoentes [veja (15)].
9. Prove a Quarta Lei dos Expoentes [veja (15)].