Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 28
Use o Teorema da Estimativa de Séries Alternadas ou a Desigualdade de Taylor para estimar a gama de valores de para os quais a aproximação dada tem precisão dentro do erro estabelecido. Verifique sua resposta graficamente.
Passo 1
E aí, pessoal! Belezinha? 😊
Nessa questão precisamos estimar os valores de da função abaixo, com uma aproximação dentro do erro estabelecido, utilizando ou o Teorema da Estimativa de Séries Alternadas ou a Desigualdade de Taylor.
Observa direitinho essa nossa função dada no enunciado. Tá vendo que ela alterna entre valores positivos e negativos? Logo, para essa questão, é mais simples usar o Teorema da Estimativa de Séries Alternadas.
Com isso, o erro de uma estimativa é menor que o próximo termo da série em módulo!
Passo 2
O cosseno da questão é basicamente o desenvolvimento da série de Maclaurin para:
Observe que o nosso erro seria menor se usarmos o próximo termo da série de Maclaurin do cosseno em módulo que seria
Ou seja,
Se queremos um erro menor que , podemos dizer que
Isolando o
Passo 3
Olhando graficamente
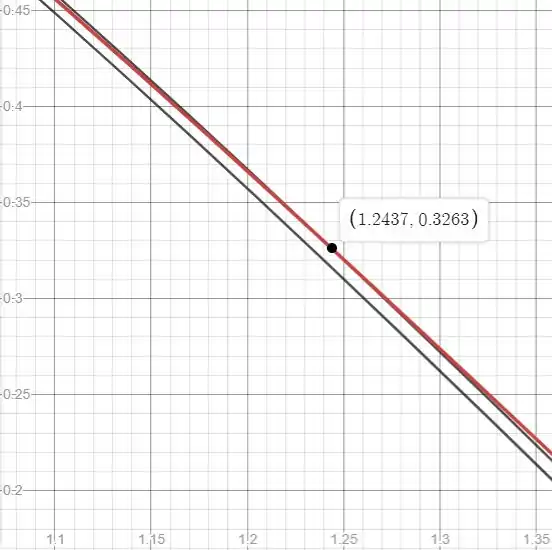
Temos em vermelho o polinômio e em preto e , que são as margens de erro aceitáveis e o polinômio encontra o limite em .
Então os valores da nossa estimativa estão dentro da margem de erro. Como a função é simétrica, o limite inferior do intervalo vai ser